투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)
covariate (공변량)
공변량이라는 변수는 독립변수라기 보다는 하나의 개념으로서 여러 변수들이 공통적으로 함께 공유하고 있는 변량을 뜻한다. 예를 들어서, 우리가 뉴럴 네트워크에 평균 0 분산 1로 규격화 된 분산을 넣어주는 것 같은 행위는 연구자가 통제하고자 하는 변수로써 이를 공변량이라 한다.
그렇다면 공변량 변화는 무엇일까? 입출력 규칙은 훈련시와 테스트시에 다르지 않지만 입력 (공변량) 의 분포가 훈련시와 test시에 다른 상황을 공변량 변화라고 부른다. (변량은 분산이랑 같은 말이고 variance임을 헷갈리지 말자. 다만 covariance 와 covarate는 다른거니까 영문 표기... 화이팅..)
internal covariate shift (ICS)
Back-propagation에 의해서 트레이닝이 진행이 되면, 특정 레이어는 해당 레이어보다 낮은 레이어가 변함에 따라 영향을 받게 됨. Network 가 깊어질수록, 더욱 스노우볼이 굴러감.
이러한 이유가 네트워크의 학습을 느리게 만들고, 파라미터 초기화에 민감해지는 이유라고 함.
즉, 특정 레이어는 인풋이 새로운 Distribution으로 계속해서 변해가는 것에 적응하며 학습해야하는 점 때문에 어려워지는 것이고, 그래서 BN을 쓰는거라는 논리 (가 있었으나 그닥 영향이 없다는 논문도 나옴).
https://ml-dnn.tistory.com/6 (internal covariate shift와 성능이 관련이 없음을 보임)
여러 Normalization들
Preliminaries
Normalization은 모델의 훈련을 효과적으로 할 수 있게 만드는 가정이다.
1. Normalization : 정규화라고도 불리며 목표는 값 범위의 차이를 왜곡시키지 않고 데이터 세트를 공통된 scale로 변경하는 것이다. (feature scaling) 대표적으로 Min-Max Scaler 가 있다. (데이터를 0~1 사이로 조정하는 방식으로 많이 쓰임)
2. Regularization : 일반화, 정규화로 불리는데 이것은 제약이라고 생각하면 편하다.
- weight decay (총 weight의 합 (혹은 제곱의 합)을 작게 만드는 기법) ,
- dropout
- pruning (가지치기. Decision tree에서 가지 개수를 줄여서 regularization 하는 것)
등이 이에 속한다.
3. Standardization
Standardization은 표준화라고 하며, Standard Scaler 또는 z-score normalization을 의미함. 기존 데이터를 평균 0 표준편차 1인 표준분포의 꼴 데이터로 만드는 것을 의미한다.

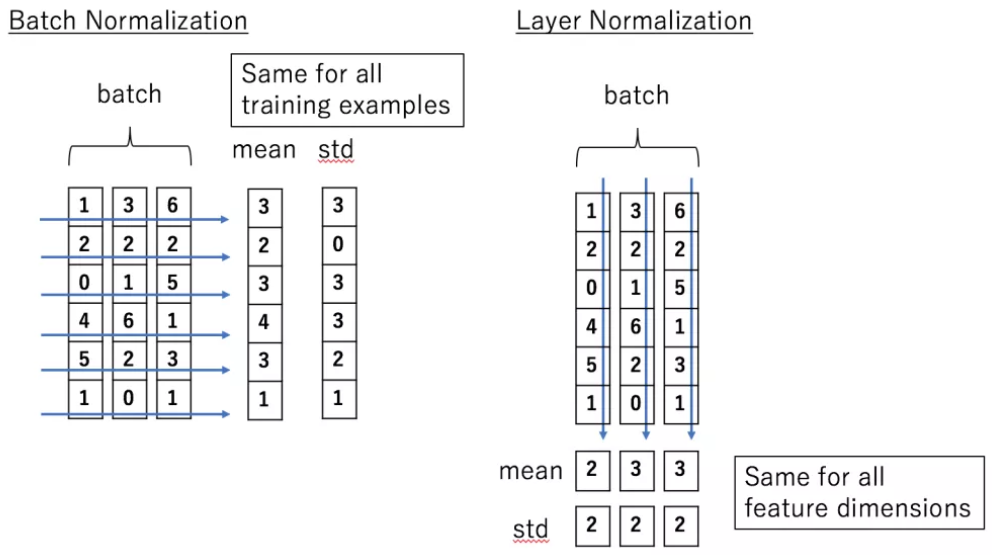
Batch Normalization :
1. batch 단위로 평균을 구함. (vector의 각 element끼리는 합치지 않고 같은 위치의 element만 평균냄)
2. 각 데이터들의 분산을 구함.
3. normalize 진행
4. scale and shift 함.
문제 : batch size가 작을 경우에는 좋지 못한 상황이 발생한다.
Layer Normalization
배치놈은 기존의 배치들을 normalization했다면, Layer normalization은 Feature 차원에서 정규화를 진행한다.

해당 feature 들의 [ i, j ] 를 변경하는 부분에 주목하자.
단 주의 할 점은, 모든 convolution filter들까지 다 ! 같이 합쳐서 정규화를 진행한다는 점이다.
Instance Normalization
instance normalization은 layer normalization과 유사하지만, 아래의 식을 보자.
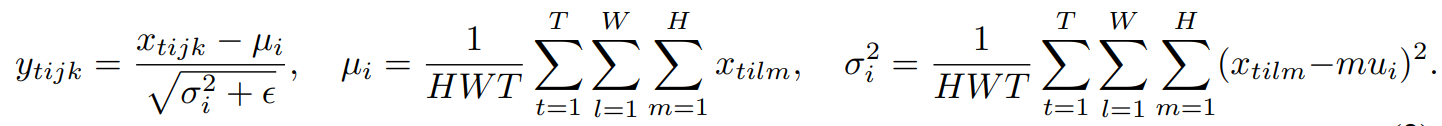

t는 각 데이터를 의미하며, 위의 instance normalization은 image data를 target한 논문이었기 떄문에 W,H는 너비 높이를 의미한다.
각 데이터마다 normalization을 따로 하고, 심지어 filter들의 종류와도 관계없이 (layer norm과의 차이점) 다 따로 normalization을 진행한다.
Group Normalization
Instance Normalization과 유사함. 다만 여기서는 채널들을 그룹으로 묶어 평균과 표준편차를 구한다.
마치 , Layer Normalization과 Instance Normalization의 중간정도라고 생각할 수 있다.
만약, 모든 채널이 하나의 그룹으로 묶여있다면 Layer Normalization 이고 모든 채널이 각각의 그룹이 되어있다면 Instance Normalization이다.
Group Normalization은 '이미지 인식 task'에서 batch size 32보다 작은 결과에 대해서는 Batch Normalization과 거의 근사하거나 나은 성능을 냈으며 큰 결과에 대해서는 좋지 못한 성능을 보여주었다.
Weight Normalization
Weight Normalization은 mini-batch를 정규화하는 것이 아니라 layer의 가중치를 정규화한다. Weight Normalization은 레이어의 가중치 w를 다음과 같이 re parameterize 시킨다.

(벡터 v의 길이는 일반적으로 || v || 또는 | v | 로 나타내며, 벡터 v에 대한 놈(norm), 길이(distance), 크기(magnitude)라고 부른다)
w 벡터의 방향으로부터 norm을 분리시킨 후 g와 v를 gradient descent하여 optimize 한다. 이것을 통해 dynamics를 배우고 최적화를 쉽게 만든다.
다만 이 방법은 평균을 0으로 보장해주지 못하기 떄문에 mean-only batch normalization과 함께 사용할 것이 권장된다.
(정리하자면, 길이 1인 unit vector + 길이 vector g를 통하여 하나의 벡터를 두개의 파라미터로 표현한다는 것)
Weight Standardization
Weight Standardization의 경우 각 conv filter의 mean을 0 , variance를 1로 조절해준다. (아래 그림 참고)

이를 수식으로 표현하면 W_i,j = ( W_i,j - mean(w_i) )/ stv_(w_i) 이 된다.
논문에서는 Weight standardization과 Group Normalization을 같이 사용하는 실험에서 BN보다 좋은 성능을 달성했다고 합니다.
참고 링크 : https://subinium.github.io/introduction-to-normalization/ (수빈갓;)
https://blog.lunit.io/2019/05/28/weight-standardization/
Lipschitzness

이때 L을 Lipschitz constant라고 하며, 이 값이 작을수록 function f가 smooth해짐을 의미한다. (그래프가 smooth 해진다면 수렴을 잘 한다는 사실은 자명하다)
Lipschitz constant는 아래와 같이 gradient의 크기에 의해 좌우됨.


