투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)
머신러닝 관련 기본적인 지식들이 먼가 개념을 제대로 정리할 필요성이 있어서 한번 싹 요약해볼라고 한다.
용어들을 듣고있자면 순간 아;; 긴가민가 이게 뭐더라 싶어서 정리한다.
+ ) 사족을 달자면 고1때 한번 쓰러지고 나서부터 계속 이렇게 빡 빡 정리해놓지 않으면 디테일한 부분에서의 기억력이 다 날아가버리기 때문에 더 신경쓰고 살아야겠다고 생각해서 ^_^....
(ratsgo 님 블로그 참고 많이..했고 포스트 너무 잘 보고있씁니다 감사합니다..)
1. Maximum Likelihood Estimation (최대 우도 추정)
최대 우도 추정이란 모수(parameter)가 미지의 θ확률분포에서 뽑은 표본 (관측한 결과) x를 바탕으로 를 추정하는 기법이다. 여기서 우도(likelihood)란 이미 주어진 표본 x들에 대해 모집단의 모수(모델이라면 파라미터) θ 의그럴듯한 정도를 나타낸다. L(θ|x) 는 (θ given x) p(x|θ) 와 (x given θ) 비례한다.
**
정리하자면, 데이터 자체의 분포는
P(x)
Likelihood는 어떤 특정 class c에 속해있는 (혹은 어떤 파라미터에서 뽑히는?) 데이터의 분포
P(x|c)
(이를 최대화하는 방법이 MLE이고, 이것을 최대화 하는 이유는 주어진 데이터 x들을 가장 잘 설명할 수 있는, 확률을 높일 수 있는 θ를 찾으면 새로운 데이터 x` 에 대해서 P(x`|θ)을 구해보고, 해당 x`에 대한 가치 판단을 할 수 있기 때문이다.)
Posterior (사후 분포)는 데이터가 들어왔을 때 해당 class 에 mapping되는 확률 분포
P(c|x)
그리고 어떤 class가 있는지에 대한 확률
P(c)
**
2. Maximum Likelihood Estimation(MLE) vs Cross entropy , KL-Divergence
우리가 가진 학습데이터의 분포를 P_data, 모델이 예측한 결과의 분포를 P_model, 모델의 모수(파라미터)를 θ라고 두면 Maximum Likelihood Estimation은 다음과 같이 쓸 수 있다. 이때 Expection 안에 log가 들어간 이유.2u는 엔지니어링 적인 이유로, 만약 1보다 확률을 지속적으로 곱한다면 언더플로우 문제가 발생하기 때문에 취하는 것이다. 다만 전체 값에 로그를 취하거나 scale 을 변화시켜도 대소는 변하지 않기 때문에 두 식이 동일한 의미를 갖게 된다.

KL-Divergence는 두 확률 분포의 차이를 계산하는데 사용하는 함수이다. 딥러닝 모델을 만들 때, P_data와 P_model간의 차이를 KLD를 사용해 구할 수 있고, KLD를 최소화하는 것이 모델의 학습 과정이 된다. KLD의 식을 보게 되면
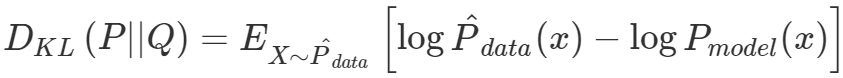
위와 같은 식이 나온다.
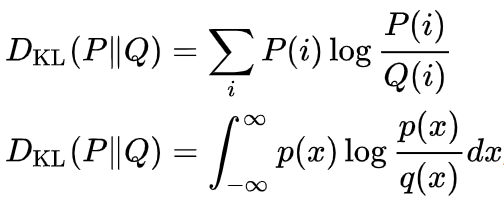
위 식의 왼쪽 term의 P는 우리가 가지고 있는 데이터의 분포를 가리키며, Q는 우리가 예측하게 되는 값이므로 오른쪽 term의 영향으로 나타나게 되는 KLD를 최소화하는 것이 우리의 목적이 된다. 위 식의 오른쪽 term (log P_model(x))이 (아래에 다시 씀) 크로스 엔트로피(cross entropy)라고 한다.
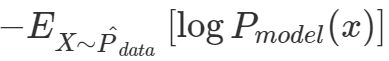
cross entropy의 식을 살펴보면 log(P_model(x))의 확률 자체가 P_data로부터 뽑은 X에 대해 P_model(x)가 그 확률(likelihood)을 최대화 하는것이 loss를 줄이게 되는 결과임을 알 수 있게 된다. 이것을 파라미터를 변경하여 확률을 최대화 하기 때문에 maximum likelihood estimation과 본질적으로 같음을 알 수 있다.
3. MLE vs Mean Squared Error(MSE)
θ_ML = arg max_θ P_model(Y|X;θ) 인 것이며 이를 log를 붙여서 arg max_θ sum(1~m) (log P_model(y_i | x_i;θ )로쓰기도한다.
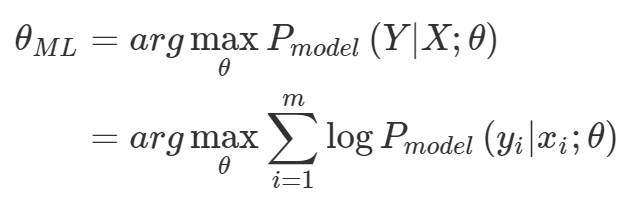
아래와 같은 상태라면 x와 y를 각각 샘플링한 결과를 최대화 한다는 말이 되기도 한다. (중요하지 않지만 몬테카를로 추정과 연관이 있기도 한 얘기엿슴 ㅎㅎ;;; )
이때!!! 우리가 많이 쓰는 평균제곱오차(Mean Squared Error)을 생각 해 보자. 그것은 다음과 같이 정의된다.
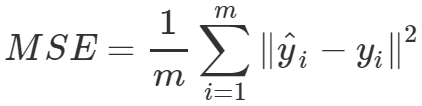
예측 y와 실제 y의 차이의 제곱의 평균. 기지? 이 식을 Linear regression에서 objective(목적 식)로 썼었다.
그리고 아까 위의 P_model 이 가우시안 확률함수라고 가정해보자. ( 다시 말해 X와 Y가 정규분포를 따를 것이라고 가정 해 보는 것이다. ) 그러면 정규분포 확률함수로부터 이 모델의 sum of log likelihood 는 아래와 같이 된다.
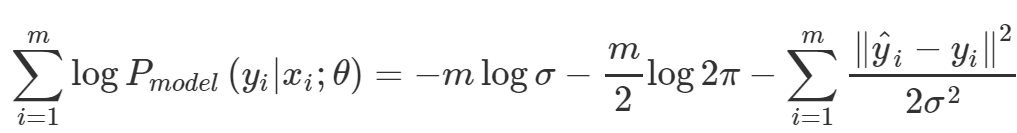
이 영롱하고 아름다운 식의 자태를 비교 해 보자. (사실 직접 식 전개는 안해봄) 왼쪽 두개 term은 모두 상수값으로 실질적인 파라미터에게 영향을 끼치는 식이 아니다. 오른쪽의 식을 보면 분산으로 나뉘어 있을 뿐 본질적으로 Mean Squared Error과 같은 식이 된다.
---------------------------------------
베이지안 확률 (Bayesian probability)
베이즈 정리라고도 불리며, 종속적, 의존적 관계에 놓인 사건들을 기반으로 확률을 구함.
P(A|B) = P(B|A) * P(A) / P(B) 가 된다.
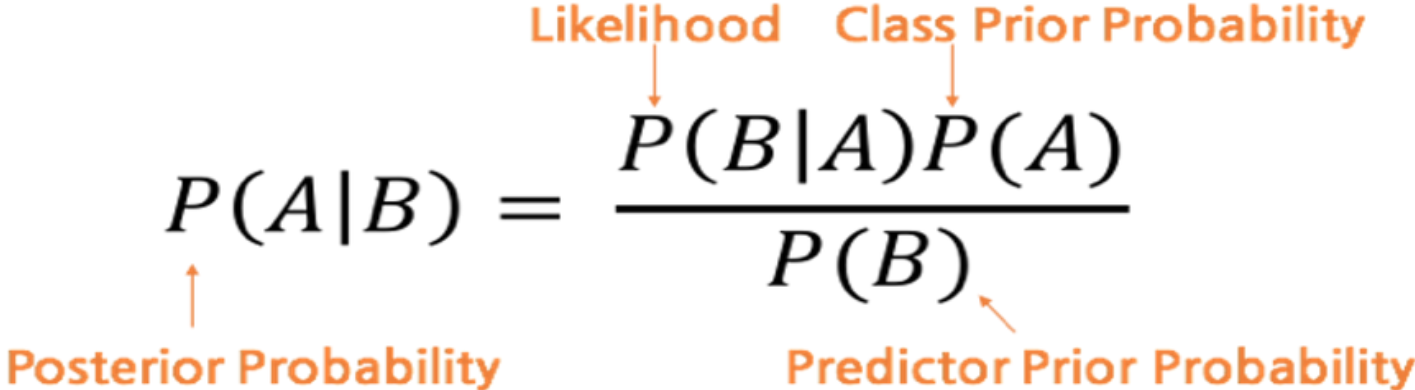
P(A)를 알고 P(B)를 아는 상태에서 P(B|A)까지 알게되면 P(A|B)를 구할 수 있다.
보통의 경우 P(A) P(B)만 알고있으며 P(B|A) (AKA likelihood)를 모델에서 구해서 P(A|B)를 추정하는 용도로 많이 쓴다.
확률 변수
확률 변수(random variable)란 다양한 값을 랜덤하게 가질 수 있는 변수(variable)이다. 확률 변수는 표본공간(sample space)에서 상태공간(state space)으로 보내는 function이며, 확률적인 과정에 따라 확률변수의 구체적인 값이 결정된다.
표본 공간이란 어떤 시행(실험)에서 나타날 수 있는 모든 결과들의 모임({X})을, 상태공간이란 해당 확률변수가 취할수 있는 모든 실수들의 집합({Y})을 나타낸다. 예를 들어 동전을 1회 던지는 실험에서 표본공간은 {앞면,뒷면}이 된다. 확률변수 X를 동전을 두번 반복해서 던졌을 때 앞면이 나온 횟수로 정의하면 상태공간은 {0,1,2}가 된다.
다시말해서 "표본공간 -> 상태공간" 으로 보내는 함수(또는 모델)라고 생각하면 조금 직관적이지 않을까....?
(근데 내가 아는 random variable랑 어째 좀 다른 것 같은 기분이 드는데 내가 잘못 알고 있던거겠찌?)
확률 분포
확률분포는 개별 확률변수나 확률변수의 집합에 대응하는 확률들의 집합을 가리킨다. 확률분포는 상태(state)가 얼마나 많이 나타나는가를 나타낸다. 식으로 말해보자면 P(state)....
이산확률변수와 확률질량함수.
이산확률변수는 상태공간이 유한집합이거나 셈할 수 있는 무한집합인 확률변수를 가리킨다. 확률 질량 함수 (probability mass function)은 확률변수의 한 상태(state)를 그 상태가 나타날 확률(0~1)로 대응시켜주는 함수이다. (확률 질량 함수는 다시말해서 이산적인 분포에서 어떤 특정 상태일 확률을 구하는 함수이다.)
만약 확률변수 X ( X : state -> 0~1 )가 x일 가능성을 수식으로 표현 해 보면

위와 같이 되는데 이를 해석하자면 X가 x일 확률은 state 에서 추출한 s에서, X(s)=x라고 답변하는 s 를 뽑을 확률이라고도 말할 수 있다.
균등분포를 예로 들어보자. 균등분포는 각 상태에 해당하는 확률이 동일한 확률분포를 가리킨다. k개의 서로 다른 상태를 가진다고 할 때 균등분포를 따르는 이산확률변수 X의 확률질량함수는 아래와 같다.

여러 확률변수에 대한 확률분포를 결합확률분포(joint probability distribution)이라고 한다.
P(X = x, Y = y) 는 확률변수 X,Y가 각각 x,y일 확률을 의미한다. P(x,y)라 적기도 한다.
아래 링크도 참고하자.
https://ko.wikipedia.org/wiki/%EA%B2%B0%ED%95%A9%EB%B6%84%ED%8F%AC
결합분포 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 둘러보기로 가기 검색하러 가기 확률론에서 결합 분포란 확률 변수가 여러 개일 때 이들을 함께 고려하는 확률 분포이다. 결합 분포는 확률 분포의 일종이므로 결합 확률 분포라고도 한다. 이산적인 경우[편집] 이산 확률 변수 X, Y에 대한 결합 확률 질량 함수는 Pr(X = x & Y = y)로 쓸 수 있다. 그러면 다음 식이 성립한다. P ( X = x a n d Y = y ) = P ( Y = y | X = x )
ko.wikipedia.org
베르누이 분포
어떤 상황(실험)이 두가지(binary)의 결과를 가질 때, 이를 베르누이 시행(bernoulli trial)이라고 한다.
일반적인 베르누이 시행에서의 시행 결과는 성공(success)또는 실패(failure)로 나타낸다. 따라서 베르누이시행의 표본공간은 {성공,실패}, 상태공간은{0,1}로 원소가 각각 두개인 집합이 된다.
* 통계학적인 관점에서 표본 공간은 확률실험에서 가능한 모든 결과를 나열하거나 표현한 것을 의미하며, 상태공간은 표본공간의 각 원소가 가지는 수치적인 특성을 나열한 공간을 의미한다.
성공을 1 실패를 0으로 대응시키는 함수를 베르누이확률변수(bernoulli random variable)이라고 하고 이 확률변수의 확률분포를 베르누이분포라고 한다. 아래와 같이 표현할 수 있다.
| x | 0 | 1 |
| P(X=x) | 1-p | p |

베르누이분포의 기대값과 분산은 다음과 같다.
(분포가 성공할 기대값이고 0 1들이 나왔을 때 그 값들의 분산이다)
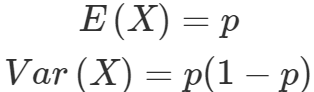
다항분포
다항분포(multinormal distribution)란 k개의 서로 다른 상태를 가질 수 있는 하나의 이산확률변수에 대한 확률분포를 가리킨다. (즉 어떤 이산확률분포의 가능한 상태가 k개라는 뜻.) 그리고 이 때 각각의 확률이 p_1,p_2,p_3,....p_k일 때 n번의 시행에서 i번째의 값이 x_i회 나타날 확률은 다음과 같다.

시행을 n번 했으므로 x_1 + ... + x_k = n이 되어야 한다. 그렇지 않을 경우의 확률값은 0으로 정의된다.
오른쪽 term의 앞쪽 곱을 보면 경우의 수에 대한 확률이며 뒷쪽은 해당 사건의 발생확률을 거듭제곱한 것을 볼 수 있다.
경우에 따라 다항분포는 값이 나타나는 횟수가 아니라 독립시행에서 나타난 값 자체를 가리키기도 한다. (다른 예시를 하나 들면 모델을 한번 돌렸을 때 그 softmax 결과?) 엄밀하게는 이러한 분포를 categorical distribution이라 한다. k개 카테고리를 분류하는 뉴럴네트워크를 만들 때 마지막 층의 출력결과물은 k-dim의 확률벡터가 될 것인데, 이 벡터의 각 요소값들은 해당 인스턴스가 각각의 범주일 확률을 나타낸다고 볼 수 있게 된다.
어떤 시행에서 k개의 서로 다른 카테고리가 있고 그 카테고리가 나타날 확률을 각각 p_1, p_2, …, p_k라 할 때 1회 시행에서 i번째 범주 c_i가 나타날 확률은 다음과 같이 표현한다.

* 가우시안 분포 = 정규분포 머리에 때려박자
-----------------------
베이즈 규칙
일반적으로 사건 A_1, A_2, A_3가 서로 배반(mutually exclusive, 동시에 존재 불가능)이고 A_1,A_2,A_3의 합집합이 표본공간(sample space)과 같으면 사건 A_1,A_2,A_3은 표본공간 S의 분할이라고 정의한다. 우리가 관심있는 사건 B가 있다고 할 때, B가 나타날 확률을 그림으로 나타내면 아래와 같다.

P(B)를 조건부확률의 정의를 이용해 다시 쓰면 아래와 같다.

P(A_1) P(A_2)와 같은 확률들은 이미 알고 있다는 뜻의 사전확률(prior probability)이라고 부르고 P(B|A_1), P(B|A_2) 등은 likelihood probability라고 부른다. (이건 우리가 관심 있는 사건이 B라서 그렇다. 딥러닝 모델에서 maximum likelihood 모델이 P(x|θ)를 최대화 하는 것을 생각해보자. )
자 그러면 B가 A1에 영향을 끼쳤을 확률, 다시말해 B일때 A1이 나타날 확률은 아래와 같은 식으로 표시가 가능하다.

P(A_1 | B)는 사건 B를 관측 후에 사건 A를 따졌다는 의미로 사후확률(posterior priority)이라고 정의된다. 사전확률에서 B라는 조건이 더해진 상태라고 생각하면 편할 것.
중심극한정리
모집단의 분포가 정규분포이다 -> 모집단에서 뽑은 표본이 정규분포를 따른다.

당연한 말이다.
모집단의 분포가 정규분포가 아닌 경우에는 이 사실이 성립하지 않지만 표본의 크기 n이 충분히 크면 그 '총 결과'의 분포가 정규분포와 가까워진다고 한다. 예를 들어 성공확률이 p인 베르누이 시행을 n번 반복할 때 성공횟수의 X분포를 이항분포라고 한다고 한다. 그러면 이항분포의 평균과 분산은 np , np(1-p)가 되는데 이 중심극한정리는 n이 충분히 크면 X가 정규분포는 따르지 않아도 표본의 분포가 평균이 np이고 분산이np(1-p)인 정규분포와 유사해 진다는 점을 알려 주는 것이다.

데이터의 특징을 나타낼 수 있는 값의 종류들
1. 평균
2. 분위수
- 예를 들어, 오름차순으로 나타냈을 때 상위 25% , 상위 75% 같은것. 영어로는 (~th percentile이라고 함)
- 제1분위수, 중앙값, 제3분위수로 25% 50% 75%를 특별하게 부르기도 한다.
3. 중앙값
4. 산포(dispersion) / 산포도
- 모집단에서 특성값이 흩어져 있는 정도를 뜻함.
- 산포에 관련된 대표적인 측도로 분산(variance)이 있다.
5. 최빈값
6. 분산과 표준편차
7. 공분산(covariance), 상관계수(correlation coefficient)
- 두 확률변수의 직선관계가 얼마나 강하고 어떤 방향인지를 나타냄
- 공분산은 두 x와 y의 dot product를 element 개수로 나눈 값으로 계산된다.
- 상관계수는 공분산의 결과를 x와 y의표준편차로 나눈 값이다.
import numpy as np
def covariance(x, y):
n = len(x)
return np.dot(de_mean(x), de_mean(y)) / (n - 1)
def correlation(x, y):
stdev_x = standard_deviation(x)
stdev_y = standard_deviation(y)
if stdev_x > 0 and stdev_y > 0:
return covariance(x, y) / stdev_x / stdev_y
else:
return 0출처는, 역시 ratsgo's blog 이다.
분포들
이항분포
성공확률이 p인 베르누이 시행을 n번 반복할 때, 성공횟수를 나타내는 확률변수 X의 분포를 이항분포(binomial distribution)이라고 한다. 이항분포의 Probability density function은 아래와 같다.
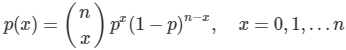
평균은 np , 분산은 np(1-p)이다.
베타분포
두 매개변수 a와 b에 대해 [0,1]에서 정의되는 연속확률분포들의 가족을 가리킨다. 베타분포의 확률밀도함수는 아래와 같다.

베타분포의 확률밀도함수는 아래와 같다.
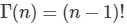
다항분포
다항분포(Multinomial distribution)란 여러개의 값을 가질 수 있는 독립 확률변수들에 대한 확률분포를 가리킨다. 여러 번의 독립시행에서 각각의 값이 특정횟수가 나타날 확률을 말한다.
자세한 설명은 글 위쪽에 동일하게 존재하므로 다시 식만 놓고간다.