투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)

Policy gradient 알고리즘은 강화학습을 학습하기 위해서 gradient ascent / descent 를 진행하는 방법에 대한 것이다.

저번주엔 reinforcement learning을 위한 object function을 만드는 방법에 대해 다뤄보았다.
partially observed 된 정책함수 πθ는 추후 다뤄보자. (지금은 fully observed만 다뤄보자)
이 πθ 에는 state가 input으로 들어가고, action이 output으로 나온다.
state는 unknown transition distribution으로부터 나오게 된다. (저 위의 globe 를 transition distribution으로 생각하면 될 것 같다)
이 수식들은 수학적으로 표현될 수 있다 pθ(τ) = p(s_1)파이(파이_세타(a_t | s_t) * p(s_t+1|s_t,a_t))
세타에 의한 궤적 확률은 시작확률 * policy로 발생하는 action에 대해 전이 확률들의 누적 곱이다.
그리고 이 모든것은 아직 알지 못한다.
최적의
세타* = arg max_세타 E_궤적 [리워드의 총합]
결국 가능한 궤적 케이스에 대한 리워드들의 총합으로 표현 된다.

어케하면 궤적의 분포에서 리워드를 최대화 할 지 생각 해 보자.

어떻게 이 주제를 평가할까?
아무런 근거가 없는데 (전이확률이나 올바른 policy도 모르는데)
그래서 오늘 저 기댓값을 추정하는 방법에 대해서 배운다.
기댓값이 취해지는 곳의 분포로부터 sample들을 만들어서 그 sample들을 average해주면 될 것 같다.
그 분포는 p_세타(tau)일 것이고 그 sample을 취하는 방법은 policy를 real world에서 acting 하게 함으로써 얻을 수 있게 된다.
예를 들어 차 운전을 50번 하게 하고 그 후 리워드를 평균내면 구할 수 있다.
(참고 : 몬테카를로 기법 / 우연 현상에 대한 통계 이용법. 난수(亂數)나 랜덤(random) 실험을 통하여 수학적인 문제의 근삿값을 얻는 방법으로, 몬테카를로의 카지노에서 행하여지는 도박의 승패 확률 계산에서 유래하였다.)
저 식의 아랫첨자 i는 indeices over the samples 이다. 1~N까지로 sum 된다.

이제 이 목적함수를 최대화 해 보자.
우리가 maximize나 minimize하고싶은 어떤 것이 있다면 그것을 위해서 최대한 노력하는 방향으로 gradient step을 할 수 있기 때문에 쵝오야.
notation의 편의를 위해서 r(tau)로 (두번째줄) 간소화 했다.
**슬라이드에서 혼용하는데, p_세타(tau) 는 파이_세타(tau)와 같은 것이다.
그런 후에 expectation을 오른쪽 인테그랄 처럼 쓸 수 있다. 모든 경로에 대한 행동확률 * 리워드의 형태로.
이제 이것을 미분하고 자 한다면, 우리는 파란색 밑줄 있는 저 인테그랄 식 처럼 식을 변형할 수 있게 된다.
그치만 파이_세타(tau)는 알지 못하는 초기 상태의 분포와 알지 못하는 전이 분포를 모두 포함하고 있는 식이기 때문.
(또한 tau에 대해서 적분을 해야 하는데 모든 tau에 대해서 적분하는 것이 불가능 하다.)
우리는 이 문제를 해결하기 위해서 파란 박스 안의 식을 이용한다.
log(f(x)) 미분은 f(x)미분 / f(x) 이기 때문이다.
이를 통해 노란 줄 쳐진 인테그랄 식으로 식을 변형하게 되면, 이 왼쪽에 파이_세타(tau)가 곱해져 있기 때문에 기댓값으로 표현할 수 있어지기 때문이다.
(E(f(x))는 sum ( p(x)f(x) ) 이기 때문.)
이를 통해 tau가 나오는 기댓값으로 식이 정리가 되는 모습을 볼 수 있다.

log pi의 gradient가 무엇인지 아직 모르기 때문에 조금 더 식을 전개해야 한다.
오른쪽 위의 식이 파이_세타(tau)가 무엇과 같은지에 대한 식이다.
이걸 양변에 log를 취하면 sum으로 표현이 가능하다.
저 오른쪽 세 terms로 결국 표현이 된다.
log(초기 분포 확률), log(변이 확률), log(정책 확률)
이제 초록 밑줄이 서로 같은거니까 왼쪽에 대입해보면 우리는 저 gradient가 실질적으로 궁금한 것이기 때문에 미분까지 적용 해 줘 보자.
sum이니까 gradient를 sum 안에 분배해줄 수 있다.
세타에 대한 미분인데 그렇기 때문에 log p(s_1) 이나 log p (s_t+1 | s_t, a_t) 는 사라진다.
그럼 가운데 남은거만 미분 해 보자.
(저 sum 둘이 괄호로 묶일 수 있는 것은 애초에 괄호로 묶인 상태였기 때문이다. 어떤 경로 한개가 주어졌을 때 리워드 따로, 그 경로가 나올 확률 따로 이기 때문; 순간 갑자기 괄호 나와서 헷갈려서 적어봤읍니다)
이제 이전과 같이 어떠한 policy를 가지고 sample 한 친구들을 가지고 열심히 기댓값을 때려맞춰보자.
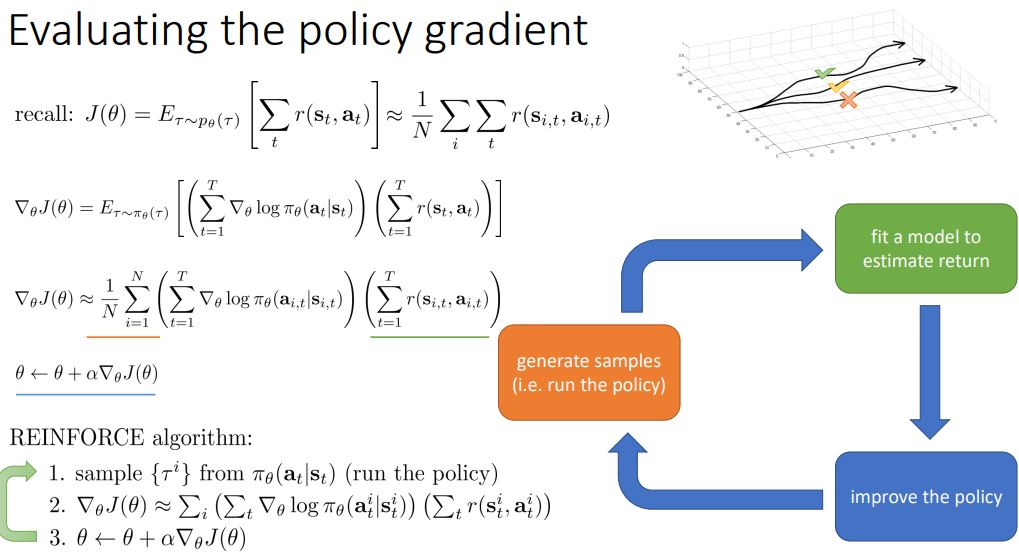
recall 부분을 보자.
J(세타)도 정확히 계산이 안되기 때문에 r(s_i,t , a_i,t) 를 N번 sample해서 평균을 내는 것으로 그 값을 추정했다.
마찬가지로 저 J(세타)를 미분한 부분도 기댓값으로 표현해놓았기 때문에 N번 샘플하여 평균을 내면 그 결과를 구할 수 있을 것이다.
N은 좀 크게 잡으라고 한다.
Reinforce 알고리즘은 결국
1. sample {tau i}(set of trajectories) from 파이_세타(a_t|s_t) / 그니까 policy를 동작시켜서 나온 어떤 순간의 state를 샘플 한다.
2. J(세타)의 세타에 대한 미분은 아까 도출한 식의 sum의 평균과 같으므로 (state i를 t때 만났을 때 action i를 t때 뽑는 것에 대해 gradient descent를 n번 한거의 평균)*(리워드) 의 평균으로 조져준다.
3. 업데이트
동작 잘 하지 않는 이유 : 분산이 넘 커서
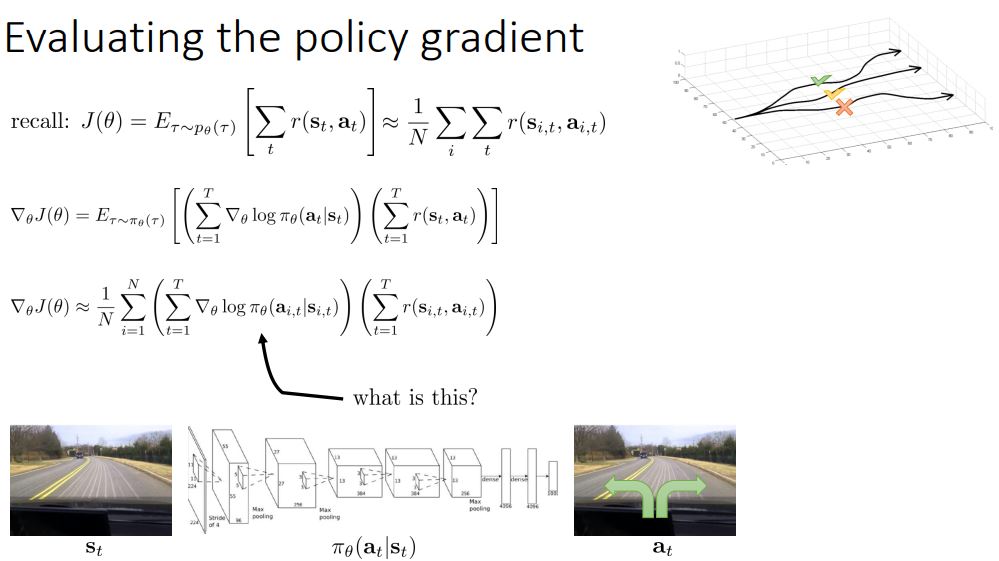
grad log(파이(a|s)) 이게 뭘까?
뉴럴넷 그림 같은 느낌일것이다.
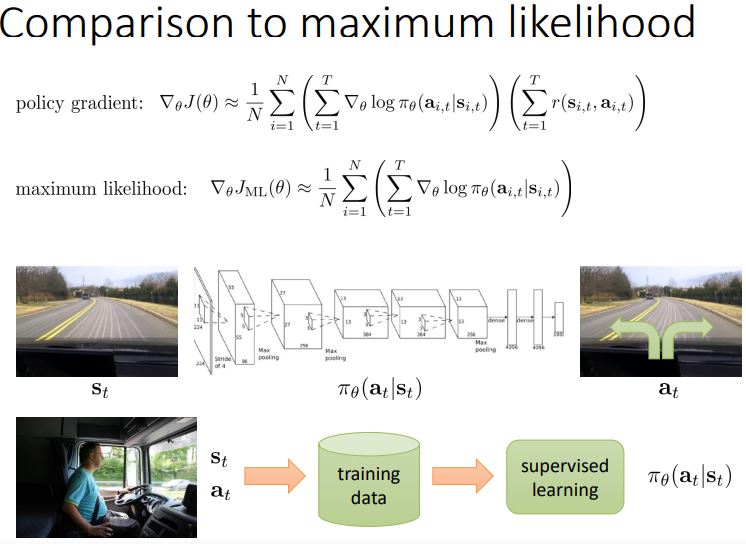
supervised learning은 maximum likelihood를 사용하여 학습 시킬 것.
-> 좋은 샘플은 증가, 나쁜 샘플은 감소.

이 연속적인 action을 생각 해 보자.
policy gradient를 통해서 저 시뮬레이팅 하는 로봇을 학습시킨다고 생각 했을 때, 이 행동은 continuous action이다. (not discrete 하다) 그렇기 때문에 우리는 파이_세타(a|s)를 통해 연속적인 값에서 어떤 분포를 찾아내야 한다.
multivariate normal distribution 도 많이 사용한다. ( 참고 : https://blog.naver.com/sw4r/221378314681 )
어... 음
그리고 그 아래는 좀 놓쳤다.
저걸 샘플링 할 때 가우시안 distribution을 쓴다는 건가?
그리고 오토인코더처럼 평균 분산을 네트워크에서 구하는거고?

이것은 수학적인 부분이고, 직관적으로 무슨 일이 벌어지고 있는지에 대해서 생각 해 보자.
결과적으로 저 수식들을 통해서 어떤 식으로 policy가 변하는 것인지 함 보자.
위 식이 우리 정택 gradient이고 이 식을 보면
저 미분 식이 의미하는 것은 더 좋은 것을 더 자주하도록, 나쁜 것을 더 조금 하도록 하고 있다는 것을 알 수 있다.
간단하게 trial and error 개념이라고 말할 수 있다.
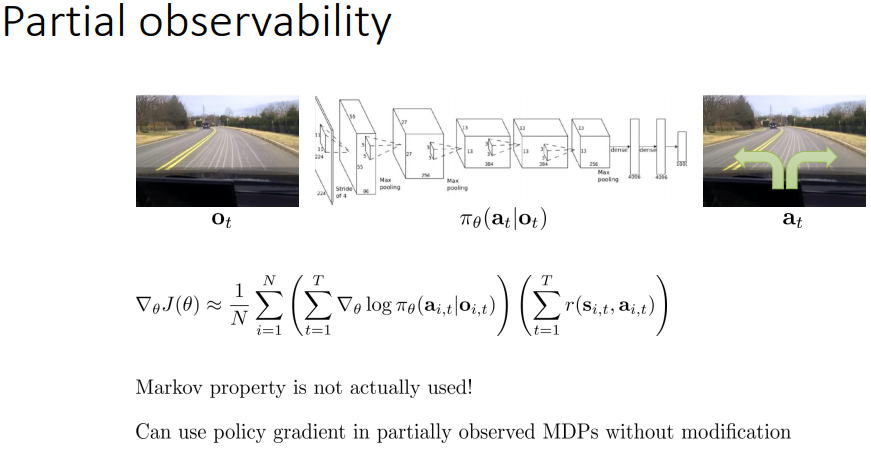
이제 다시 부분만 볼 수 있는 곳으로 돌아오자.
policy gradient도 여기서 적용할 수 있을까?
마르코프 특성은 실제로 사용 되지는 않는다.
그치만 정책 자체는 state 자체를 observation으로 변경함으로써 해결되기는 한다.
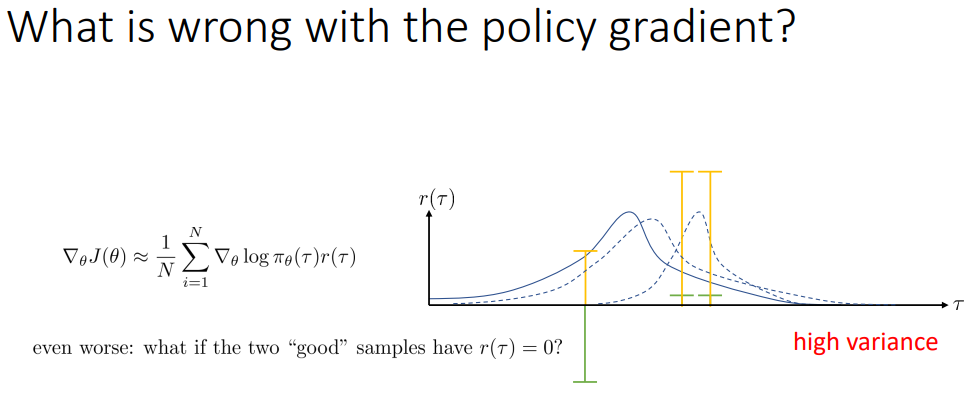
왜 아까 policy gradient가 그 자체만으로는 잘 동작하지 않는다고 했었는지에 대해서 설명 하겠다.
우리가 가우시안으로부터 추출되는 정책을 가지고 있다고 하자.
그러면 어떤 샘플들로부터 reward가 어떻게 나오느냐에 따라서 ;
머 여튼 분산이 존내 커서 (다양한 값이 나올 가능성이 존내 커서) 그 solution이 이상적이지 않게 수렴할 것이라는 말.
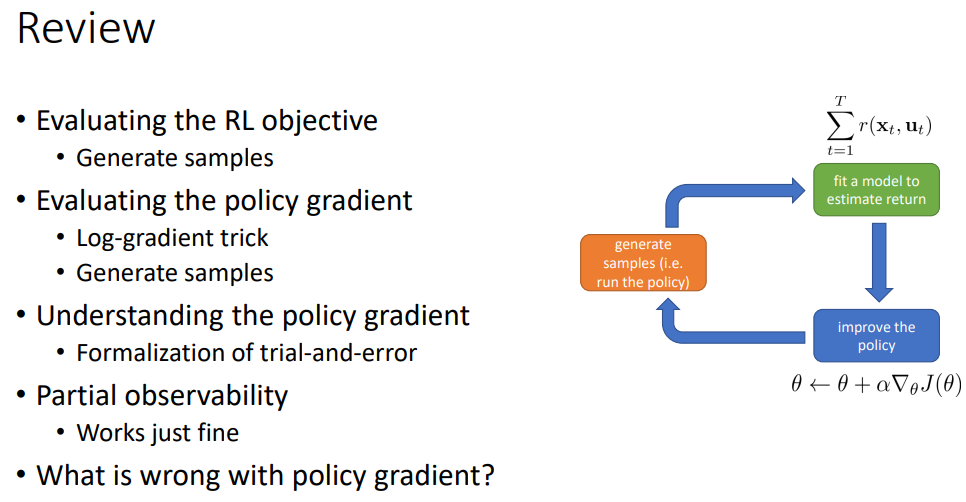
RL 목적 함수에 대한 평가
-> 샘플들을 생성해서.
Policy gradient에 대한 평가
-> log-gradient 트릭 후
-> 샘플들을 생성해서
Policy gradient에 대한 이해
-> trial - and - error을 통한 형태
Partial observability
-> state->observation으로 변경해놓고 걍 돌리면 됨.
Policy gradient에 무슨 문제가...?

이제 그 문제를 해결 해 보자.
variance를 줄이는 방법과 policy gradient에 관하여 얘기 해 보자.
처음 분산을 줄이기 위해사 사용하는 방법은 과거가 미래에 영향을 미치지만 미래는 과거에 영향을 미치지 않는다는 것이다. (causality를 보자)
그래서 우리는 과거의 리워드가 아니라 지금과 미래의 리워드만을 사용 할 것이다.
이게 분산을 줄여주는 이유는 리워드 자체가 줄어들기 때문에 분산이 줄어든다.

이제 reward를 위한 새로운 파라미터 t`을 도입해도 상관없다. 왜냐하면 저 괄호 안의 친구들이 원 식에서 서로 독립적으로 계산되기 때문이다.
이 위의 식은 log_파이 들의 합으로 표현될 수 있게 된다.이제 t=1~T까지 움직이는 이 식이랑 t`=1~T까지로 나눴다.
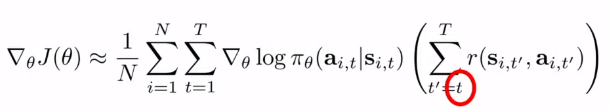
이제 리워드 타임의 t를바꿔본다.reward에대한t=1에서 t`=t로. 왜냐하면 시간 t일 때 하는 action은 시간 1~t-1까지의 reward와는 전혀 무관하기 때문이다. 이는 여전히 policy gradient를 위한 unbiased 된 측정기라고 생각할 수 있게 된다.
그러면 이제 더 작은 리워드 숫자들을 통해서 분산이 생겨서 도움이 된다.

이제 이 부분을 Q hat _i,t 라고 줄여서 부르도록 하자. 미래의 리워드 함수이다.
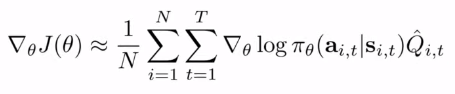
그럼 이런 식이 되겠지.

또한 두번째 도와주는 트릭 baselines가 있다.
좋은건 더 하고 나쁜건 덜 한다. 라는 거지만 사실 좋은거는 100만1 나쁜거는 99만9999 일 경우를 생각 해 보자.
이거는 좋은거와 나쁜거의 구분이 잘 안된다.
그래서 리워드에 평균을 뺀 것을 이용해부리자.
다만, 그게 가능한가? 수학적으로 맞나?
가능하다.
세번째 줄 전개되는걸 쭉 보자.
새로 만든 term을 수식적으로 전개해보자. (b가 포함된 식)
이걸 인테그랄로 바꾸고 싹 싹 오른쪽으로 바꿔나가면 결국 0이 되는걸 볼 수 있다.
(ㅎㅎ 근데 그냥 값에서 constant 뺀거니 사실상 미분해도 영향이 없는게 당연)
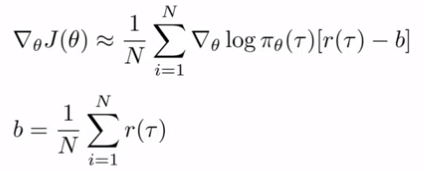

gradient는 바꾸지 않지만 variance는 바꾼다 !
식 전개 읽으삼.
(직관적으로, 제곱의 평균 빼기 평균의 제곱인데, 평균이 100만이면 100만1과 99만9999의 제곱의 차이가 -1과 1의 제곱의 차이보다 크잖!)
이론적으로 분산을 최소화하는 baseline은 맨 아래의 b이다.
그러나 average 도 just fine하다.
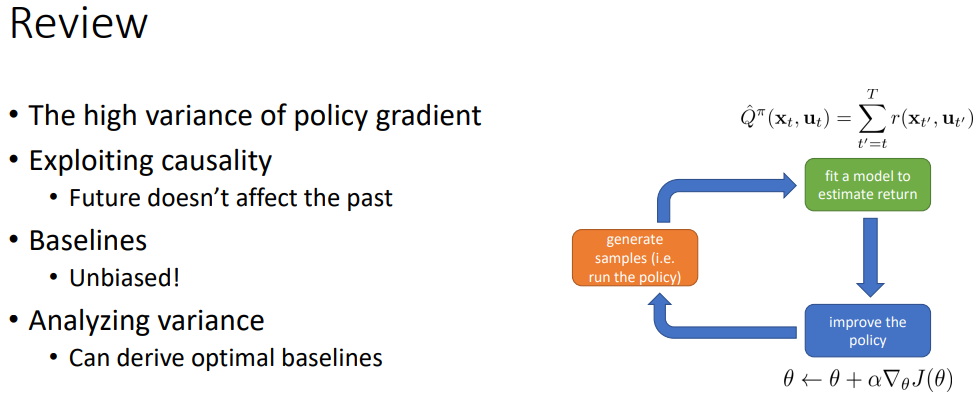
policy gradient가 분산이 높은 이유
+ 등등 배웠다.

남은 강의 동안에는 policy gradient가 어떻게 on-policy가 되는지에 대해 다룰 것이며 이것에 대해 무엇을 할 수 있는지 다룰 것이다.
on - policy : policy가 변경되면 더이상 예전의 샘플들을 사용할 수 없는 경우를 말한다. gradient update가 진행되고 나면 새로운 샘플링을 해야 함.
왜냐면 policy gradient가 세타에 의조나는 Expation of tau 로 부터 나온 것이기 때문이다.
reinforce algorithm은 step 1에서 샘플링을 하는데 이걸 건너 뛸 수가 없게 되는 것.
(그렇게 되면 expensive 한 sample들은 학습 시키는데에 답이 없게 된다.)

이때 우리가 할 수 있는 것이 있다.
우리는 policy gradient 를 어떤 off policy 알고리즘에 끼워넣을 수 있다.
(강사님은 이걸 textbook policy 라고 부른다고 한다)
실제로는 우리는 policy가 어떤지에 대해서 논할 수 있지만 원칙적으로 이것은 off-policy 이다.
우리는 이것을 중요한 sampling을 통해 할 것이다.
우리가 samples from 파이_세타(tau)가 없다면 어떻게 할까?
-> 다른 policy의 sample을 가져온다.
(오른쪽 초록 사각형) q(x)를 통해서 p(x)에 디펜던트 되어있던 식을 q(x)에 디펜던트 되게 바꿨다.
이 스킬을 이용하면 J(세타) = 새로운 파이bar을 사용해서 만든 새로운 식이 된다
unpack해 보자. (아랫줄)
그리고 이것 저것 지워보며는, 결국 맨 마지막 식이 된다.

우리는 하나의 유도를 강의 시작 부분에 다뤘고, 이제 중요한 샘플링을 다루는 약간 다른 유도를 보여줄 것이다.
일단 우리의 목적 value를 가지고, 새로운 파라미터 세타`를 통해 표현 해 볼 것이다.
J(세타)=≈≈의식이좋은게,새로운세타은 기댓값 안의 분자에만 영향을 끼치고 tau를 샘플링 하는 쪽이라던지 분모에는 영향을 끼치지 않는다. 미분하며는 그 아랫줄의 오른쪽이 되고, 만약 지역적으로 세타 = 세타`같은 곳이 있다면 결국 우리는 예전 우리가 봤던 그 식으로 돌아올 수 있으며 이론적으로는 off policy 된 상태가 된다.

그치만 당연히 세타와 세타`가 다를 경우에는 다시 다뤄야 겠다.
그리고 실질적인 off-policy policy gradient를 이뤄내야 한다.
밑에서 두번 째 줄 식을 보면, 다를 경우의 식을 쭉 전개 한 것이고 이렇게 진행하는게 잘못 된 이유가 뭘까?
T가 클 경우에는 저 확률 곱하는 첫 항이 엄청 커지거나 엄청 작아질 수 있기 때문이다.
여기에 더해서 인과관계를 통한 트릭(t` = t 부터 시작하게 하는 것)을 사용할 수 있는데 이래도 근본적인 문제는 벗어나지 못한다. (X표 친 부분의 식이 추가돼서 오히려 더욱 ;;)
그렇다면 그냥 저 맨 오른쪽 확률 곱하는 부분을 1로 만들어 버리면.. 동작 자체는 더 잘 할 것이다. 다른 이유로 다른 목적함수를 최적화 하는 것이긴 하겠지만. 이걸 통해서는 policy iteration algorithm을 얻는 것이다. (강의 후반에 다룬다)
여튼 저 세팅을 통하면 다른 목적함수이기는 하지만 policy 를 improve 하는 상황이라는 것 자체는 의심의 여지가 없다.
그럼 아직 해결 안된 저 가운데 부분을 보자.

우리가 할 수 있는 것은
first-order approximation이다.
추후에 왜 이렇게 불리는지는 알려 주겠지만 일단은 실행하려면 아이디어는 알아야 하니 무엇인지부터 알려 주겠다.
objective를 조금 다르게 써 보자.
on-policy policy gradient의 식을 보자.
이전에 Q hat 으로 표현했었던 리워드 표현 함수 Q를 추정하는 이 친구는 (s_i,t , a_i,t)를 state action marginal(정책함수)에서 뽑은게 필요했었다.
(주변 확률 분포(marginal distribution)설명 링크 https://presidentlee.tistory.com/entry/marginal-probability-distribution%EC%A3%BC%EB%B3%80%ED%99%95%EB%A5%A0%EB%B6%84%ED%8F%AC 쉽게 말해 싹 다 합한거)
이를 봤을 떄, 그 아래 세타에대한목적함수는새로운파이세타에 관한 식이 필요하다.
그렇게 state , action term을 조건부 확률로 일단 바꿔주고, 앞쪽을 무시해버린(!!!!)다. 세타`이 세타와 비슷하다면 1이라는 게 그 이유;;
근데 실제로 거의 비슷해서 그 영향은 미비하고, 이걸 무시하지 않는 연구를 6년전에 했다가 교수가 피봤다고 ;; ㅋㅋㅋ
(이 짓을 지금 진행하고 있는 이유가 과거의 샘플들도 갖다 쓰고 싶기 때문이다)

저 밑줄 부분을 전부 grad log(파이~) 다 계산하고 sum을 계산하는 과정은 굉장히 느리고 비효율적이기 때문에 standard automatic 미분 패키지에서 편리하게 실행할 수 있는 방법이 있다.
우리는 우리의 자동 미분 소프트웨어 안에서 그 그래프의 gradient가 policy gradient인 그래프를 만들 것이다.
올바른 강화학습 목표함수는 enviornment와 상호작용 해야 하기 때문에 그 그래프 자체는 올바른 강화학습 목표함수가 아니겠지만 우리는 그 gradient가 올바른 gradient가 되도록 설계 할 것이다.
그를 위해서 우리는 maximum likelihood 수식을 살펴 봐야 한다.
위의 maximum likelihood 수식을 실행하는 것을 통해 policy gradient를 실행하는 것으로 변형시켜야 한다.
weighted maximum likelihood같은 pseudo-loss를 구현.
- cross entropy(discrete (이산적인 액션에 대해))
- squared error(gaussian (연속적인?))
수도 코드로 확실하게 알아보자.

오리지날 maximum likelihood
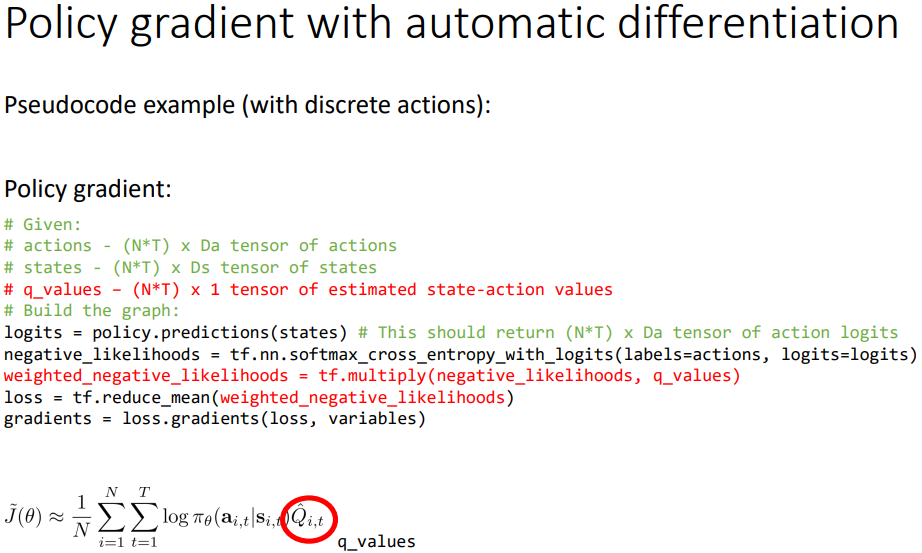
이제 식의 Q function을 위 줄과 같이 잘 작성해서 곱하면 된다. (리워드 역할)
(baseline 트릭을 추가하고 싶다면 q_values 에다가 빼면 된다)

분산 존내 높다. batch 높게 잡아라.
adam 이 ok 아마 도~

대충 리뷰한다는 내용.


