투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)


오늘은 행동에 대한 supervised learning(지도학습) 을 알아 볼 것이다.

오늘 공부할 것.
1. 순차적 의사결정 문제
2. 모방 학습 : 의사결정을 위한 지도학습
a 직접 모방이 잘 동작하는가?
b 더 자주 잘 동작하게 만들 수 있는가?
3. 약간의 이론
4. case study
목표 :
정의 이해 , 표기법 이해
기본 모방 알고리즘 이해
이론적인 분석을 위한 tools 이해

우리가 이미지 분별기를 만들고 싶다고 하자.
표기 : 이미지, (o) classes (a) 그리고 이걸 해결하는 모델 (파이(a|o))
이미지는 observation, label을 action 이라고 말하도록 하자.
guessing하는 것을 action으로 생각하기.
파이는 observation이 일어났을 때의 action 이라고 보자.
우리는 순차적 의사결정 문제(sequential decision making problem)로 변경하기 위해 모든 곳에 t라는 아래 첨자를 추가할 것이다.
time step t에 본 것이라고 생각하는 것.
더 흥미로운 것은 실질적인 sequential problem들은 어떤 action을 했냐에 따라 그 다음에 무엇을 observate 할지에 대해 의존 관계가 있다. 단순히 구글에서 이미지를 찾는거면 그렇지 않지만 정글에서 찾는(본)다고 한다면 그렇지 않을 것이다.
여기에서 위의 조건부 확률 파이의 경우 policy라고 부른다. 흥미롭게도 가끔은 deterministic(결정론적) policy를 생각할 수 있기도 하다 (하나만 1 나머지 0). 또 가끔은 observation이 아닌 state라는 것에서 정보를 얻기도 한다. 이 둘의 차이는 observation은 직접 본 장면 자체이다 (state의 lossy consequence(손실된 결과)) 그렇지만 state는 모든 특성을 요약한 것임. (치타는 차 뒤에 가려져 있는데 그것조차 알고 있으며 추가적인 정보 포함이 가능한 것이 state)
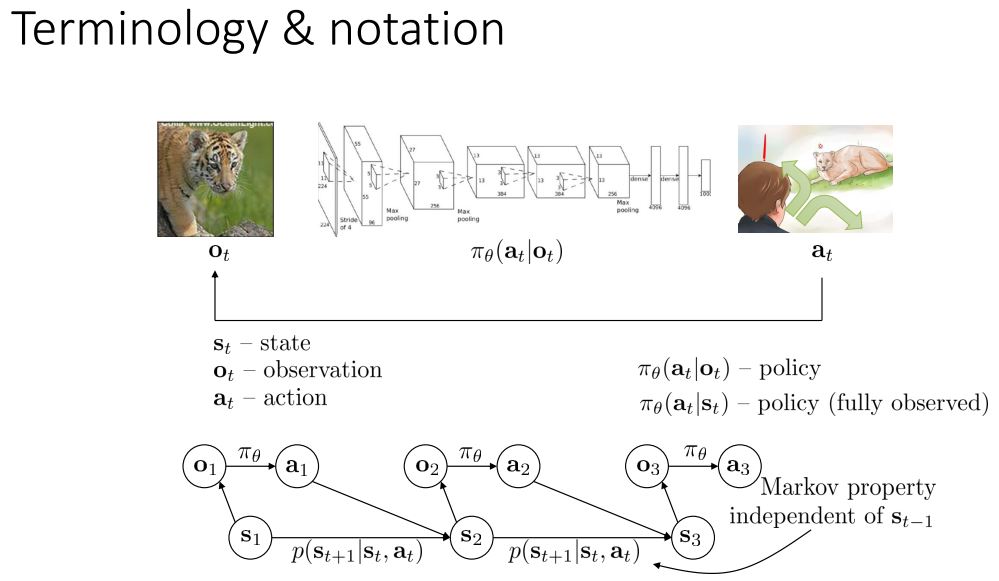
요기 아래 오토마타를 보면 더 직관적인 이해가 쉽다.
마르코프 체인을 보며는 댄다.
아까 설명한 개념에 있어서 추가적으로 p(s_t+1 | s_t,a_t)가 있는데 이는 state , action이 있을 때 그 다음 state를 예측하는 확률이다. (이것을 마르코프 확률이라고 하는데 마르코프 확률은 s_t-1 에는 의존하지 않는다. 그게 한계이긴 함.)

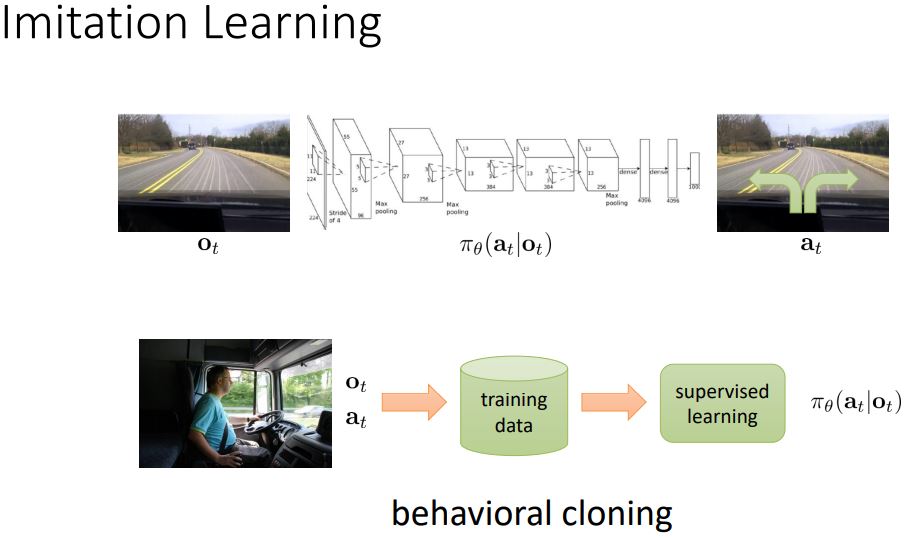
드라이버가 운전을 하면서 카메라 녹화 및 steering wheel(핸들)을 recording.
그리고 이 튜플을 dataset으로 구성한다.
그리고 비슷한 이미지에 대해서 같은 action을 하도록 하는 것이 목표이다.
그치만 잘 동작하지 않을 것이다.
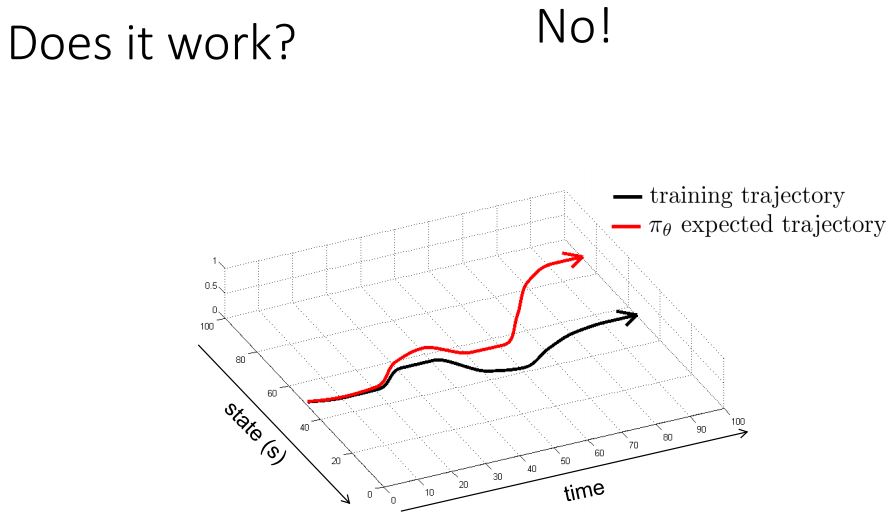
여러 이유가 있을 것이지만 우선 다양성에 대한 적응을 하지 못할 것이다. 처음엔 잘 동작하는듯보여도 곧 그 real world에 대한 분산에 대해 적응을 못 할 것이다. (는 내 생각) 여튼 작은 차이가 쌓여서 결국 큰 차이를 가져온다는게 설명의 논지였다.

그치만 3천마일정도 학습하고는, 어느정도 성공을 보였다고 하는데 그 이유는 다음과 같았다.
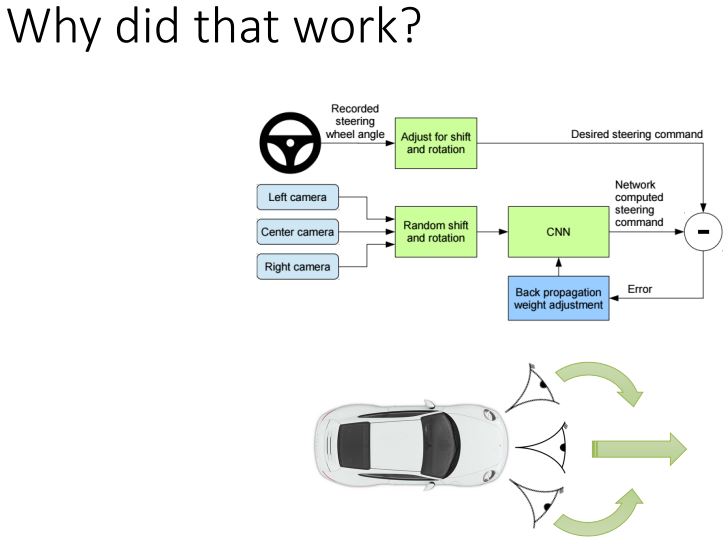
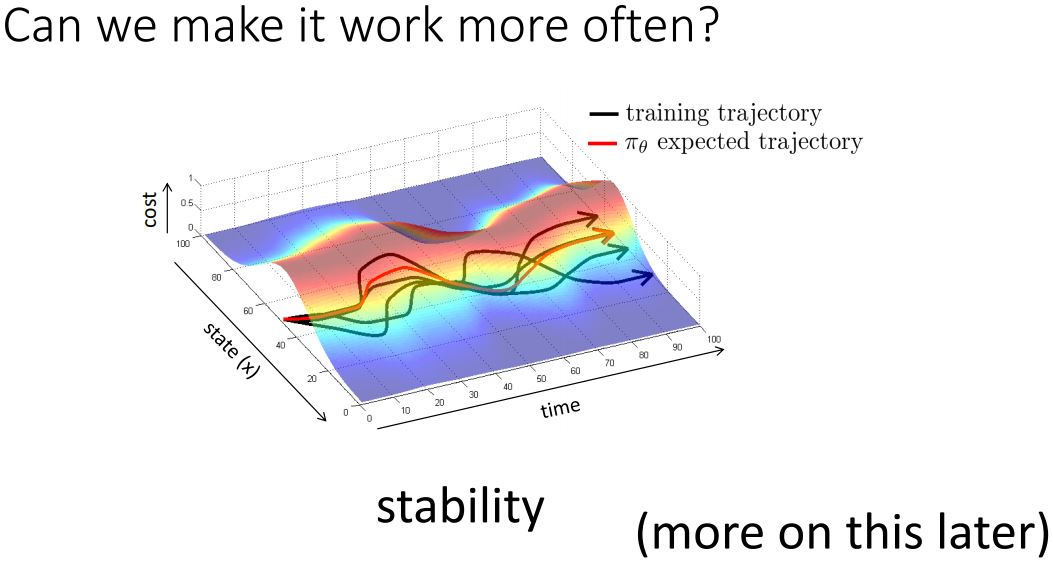
잘 동작하기 위해서 카메라를 추가로 설치했다.
각 카메라에서 발생하는 입력을 동시에 받아서 안정성을 확보했고, 이를 통해 조금씩의 벗어남이 발생할 때 recover이 된다.
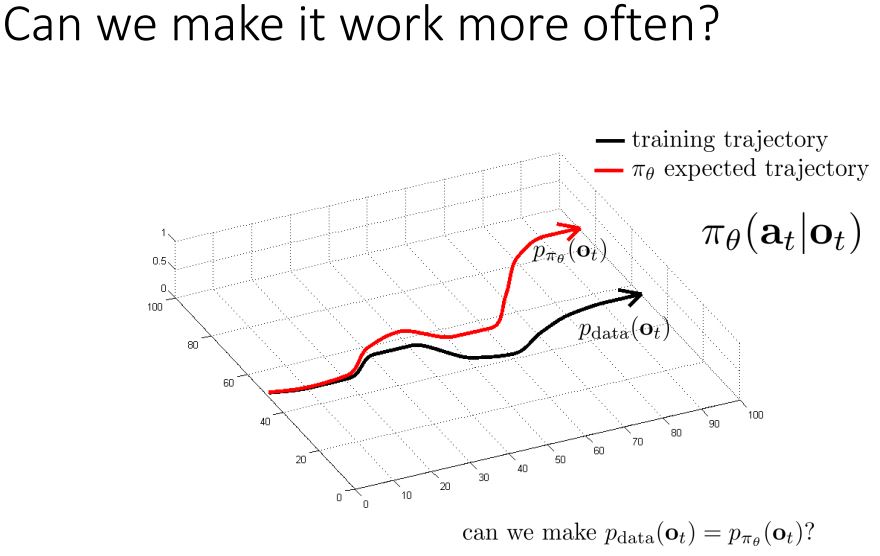
더욱 직접적인 수학적 설명을 한다.
직관적으로 행동을 그대로 따라하는 문제는 조금의 문제가 더욱 스노우볼링이 된다는 것이다.
그걸 조금 더 일반화해보자.
training data를 확보할 때, training data의 observation이 어떤 분포로부터 얻어지는 것을 생각해볼 수 있을 것이다.
이 분포를 pdata(o)라고 하자.
얻어지는 데이터는 p_data(o)로부터 샘플링 되는 것이라고 생각하는 것이다.
당연히 이 o는 서로 독립적이지 않다. 서로가 이전에 일어난 상태에서 다음에 일어난 상태로 넘어가기 때문이다.
그렇지만 supervise model에서는 우리는 이 데이터를 샘플링하기 때문에 그 부분은 무시한다.
우리는 이 데이터를 사용해서 πθ(a|o)를 학습시키는 데에 사용한다.
그리고 이걸 πθ(a|o)를 실행(action을 얻기 위해 파이_세타 에서 샘플 후 action을 적용하고 그 다음에 무슨 일이 일어나는지 보는 것) 하고 나면,
새로운 observation을 얻을 것이다.
그런 후에, 우리는 다른(pπθ(o)) observation을 받을 것이다. 어떤 다른점인지는 모르지만 다른 행동을 했으니 다른 결과를 얻을 것이다.
문제는 pπθ 는 pdata 와 다르다.
같은 data 분포에서는 트레이닝을 하면 잘 동작할 것이라는 것을 알지만 다른 분포에서는 잘 동작할지 모른다.
그러나, 우리는 다른 데이터 분포에서 모델을 평가하게 된다.
이것이 cloning 이 이론적으로 동작하지 않는 이유이기도 하다.
그렇다면 pdata 를 pπθ 로 바꿀 수 있을까?
그렇다면 우리가 데이터를 수집하는 pπθ가 pdata 가 되니 데이터 분포 문제가 사라지고, 원칙적으로 잘 동작 할 것이기 때문.

우리는 실질적으로 정책(policy)을 데이터만큼 많이 바꾸지 않을 것이다.
우리는 pπθ 말고 pdata 에 대해 조금 더 신경을 써 보려고 한다.
DAgger이라는 알고리즘인데 목표는 pdata대신 pπθ 에서 training data를 모은다.
그렇게 된다면 training과 testing이 같아질 것이기 때문이다.
어떻게?
πθ(at|ot) 를 돌리기만 하면 된다.
그치만 at라는 레이블이 필요하다.
1. Human data D={o_1,a_1, .. o_N,a_N} 으로부터 train 파이_세타(a_t|o_t) 하기.
2. 우리의 policy 파이_세타를 실행하여 데이터셋 D_파이 = {o_1,....o_M}을 얻기 (그니까 실질적으로 파이세타를 실행하면서 얻어지는 observation을 사용)
3. 여기서 얻어지는 observation들을 사람에게 질문 (ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ)
4. 이 데이터를 합친다(aggregate)

당연히 여기서의 문제는 step 3이다. 사람이 어케 다 데이터를 공부하게 하누;;
특히 체스 게임이라던지 드라이빙같은 경우에는 실질적인 좋은 판단이 어떤것인지 정의하기 힘들다.

왜 전문가를 그대로 따라하는 것이 실패할까?
1. Non-Markovian behavior
2. Multimodal behavior
두가지 문제가 있다.
1. 파이_세타(a|o)는 현재 관찰'만'을 바탕으로 action을 결정하는데, 이것은 부자연스러운 것이다. 이전 상태의 정보에 따라 다른 행동을 할 수 있기 때문이다.
따라서 더 나은 모델은 과거의 관찰들을 바탕으로 action의 분포를 제공해주는 형태일 것이다.
만약 그런다면 우리는 이 패턴들에 대해 설명(account for) 할 수 있기 때문이다.
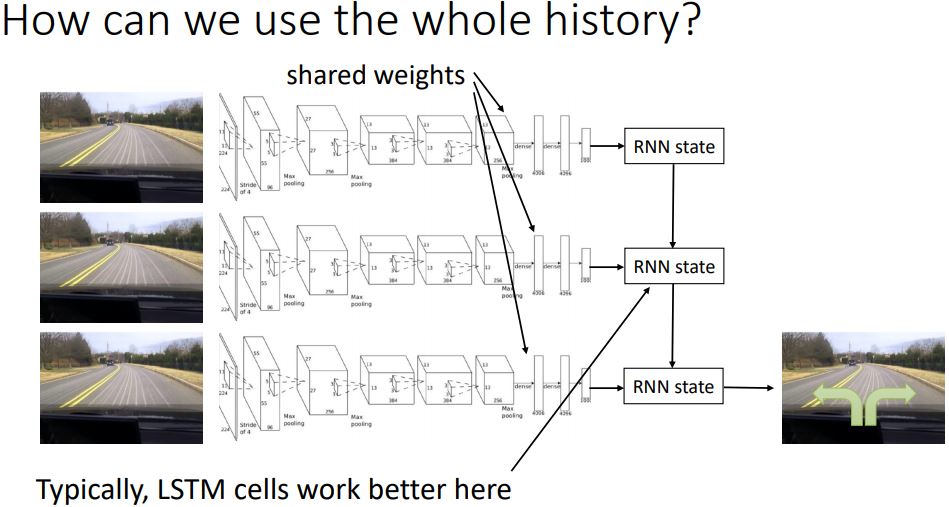
이 해결방법은 RNN을 사용하는 것이다.
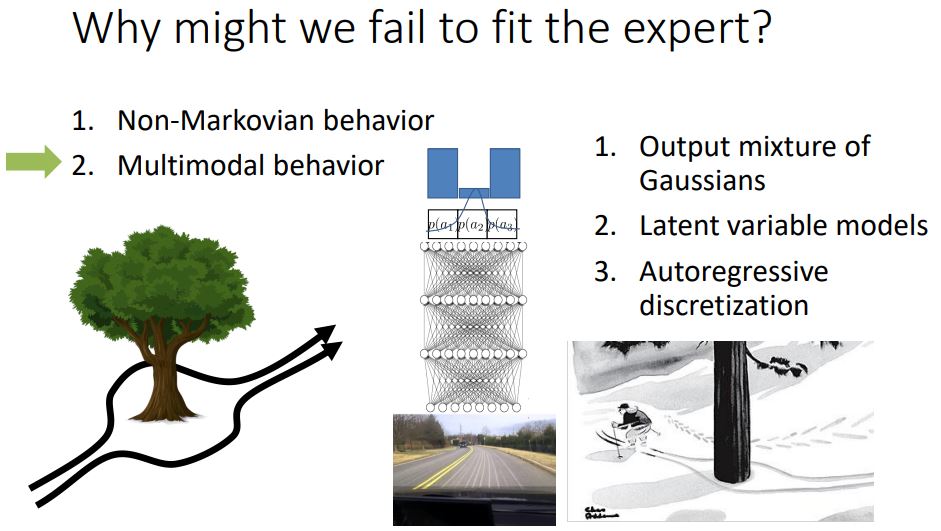
2. 같은 state가 주어지더라도 다양한 행동이 존재할 수 있다.
왼쪽가는거랑 오른쪽 가는걸 평균내버리면 가운데로 가버림 ㅎㅎ;;
해결책
1. output mixture of gaussians

n개의 normal distribution들을 뽑아냄으로써 왼쪽 오른쪽 돌아간다.
최대 n개의 경우 밖에 뽑아내지 못한다는 단점이 있지만 여전히 잘 동작할 것이다.
2. latent variable models

얘네는 너네가 원하는 정도로 표현은 가능한데 훈련시키기가 힘들다
output을 바꾸기 보다는 input을 바꾼다. 추가적인 variable (위의 normal distribution 같은?) 을 sample하고 output of the network를 얻은 후 다른 input으로 넣는다.
실 례가 궁금하다면
Conditional VAE
Normalizing flow
Stein variational gradient descent
등을 참고하라
3. autoregressive discretization
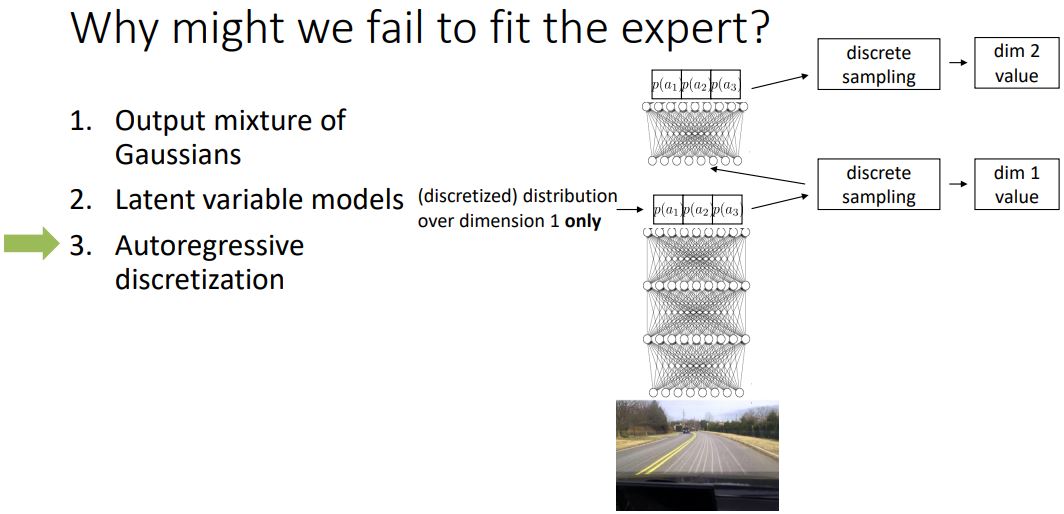
이 아이디어는, 만약 당신이 굉장히 작은 차원의 action space가 있다면 그 action space 가 연속적이라도 이산적으로 바꿀 수 있다. softmax를 통해 이산화된 확률분포를 뽑아낸다. 이 확률분포를 통해 샘플링을 한다. 또다른 네트워크에 입력으로 넣어주고 다시한번 확률분포를 뽑아낸다. (첫번째 뽑아준 값을 condition으로 하여 두번째 값을 뽑아내는 셈이다.) 이 과정을 n번 반복하여 n dimension의 출력을 뽑아내게 된다. 그러니까, 한번에 한 dimension의 value만 뽑아내는 셈
recap
결국 이 방법(따라하기)만으로는 주로 불충분하다.

이 사진으로 왔을때, 사실 우리가 원하는 것은 사자에게 잡아먹히지 않는 것이다. (저 위 식의 기댓값을 낮추는 것이다.)
어떤 정책 세타가 기댓값을 낮췄으면 좋겠는데, 그때 어떤 미래의 상태 s가확률적으로발생할수있고,그상태에서그게잡아먹히는상태일확률이다.동시에s은 (s,a)일때 s`이 발생활 확률과 연관되어 있고 action a는 모델에 의해 그보다 먼저 결정된다.
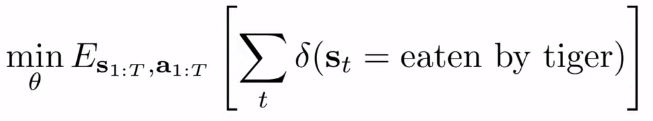
그리고 사실 더 정확히는 오늘도 내일도 모레도 잡아먹히지 않는것을 원할 것이다.
그럼 위처럼 식을 쓸 수 있게 된다.
이 식은 더욱 강화학습 문제와 비슷하게 된다.
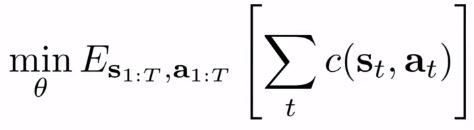
이것을 더욱 더 수학적으로 만들어보면 cost function으로 만들 수 있게 된다. (다음 강의에 제대로 다룰 것.)

대충 cost function 포함된 식에 대한 표기법
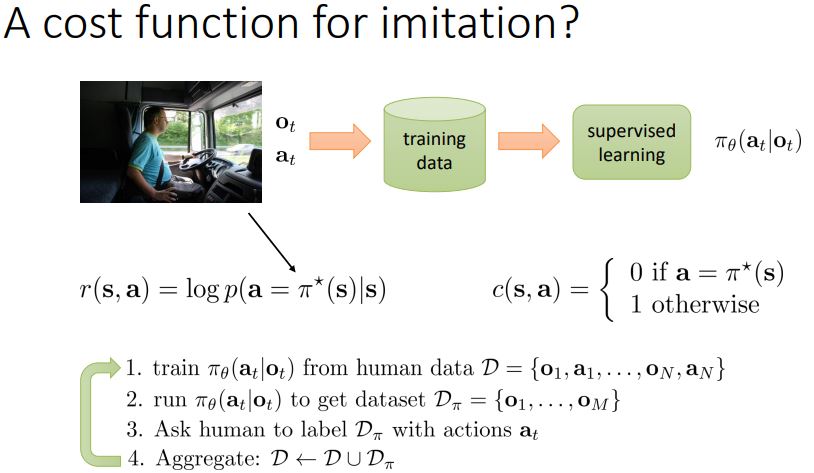
이미테이션을 위한 cost function을 정의할 수 있을까?
리워드 함수를 log p(a=파이*(s) | s) 로 하면 어떨까?
cost function을 a = 파이*(s) 일때 0 아니면 1 이라고 해도 될 것.


