투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)
ㅠ 다시한번 말씀드리지만 제 글만 가지고는 이해가 힘드실 수 있으니 강의를 켜놓고 같이 겸사겸사 보시는걸 추천드립니다... 저도 이해가 다 안가요..................................... 잘 아시는분은 댓글로 설명좀 부탁드릴게요.......

이번 부터는 continuous data에 대해서 동작할 flow-based models에 대해 배워 볼 것이다.

여태까지 배운것을 포함해서, 이 강의가 끝나면 어떤 것을 얻어가야 할까?
우리가 likelihood based model을 배울것이라고 하면, 그 중에 어떤 것을 얻어가는 것이 중요할까?
일단 train이 빠르게 잘 되며, sample이 빠르게 잘 되는 것을 원할 것이다.
이걸 compression문제에 가져오면, 우리는 compress가 빠르며 decompress가 빠른 것을 원할 것이다.
그리고 단순히 빠른 것 뿐만 아니라, 압축 자체도 잘 동작해야 할 것이다.

그렇다면 도대체 flow란 무엇일까?
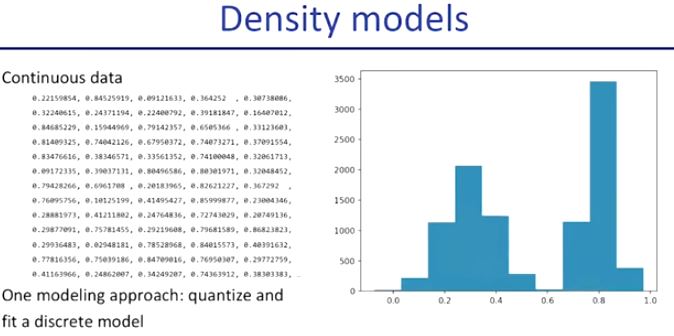
flow에 들어가기에 앞서 continous data란 위와 같이 연속적인 실수들로 이루어진 data를 continous data라고 한다.
그리고 오른쪽 그림과 같이 histogram등의 방법이나 autoregressive model 등의 방법을 통해서 처리를 하는 방법에 대해 다뤄보았었다.
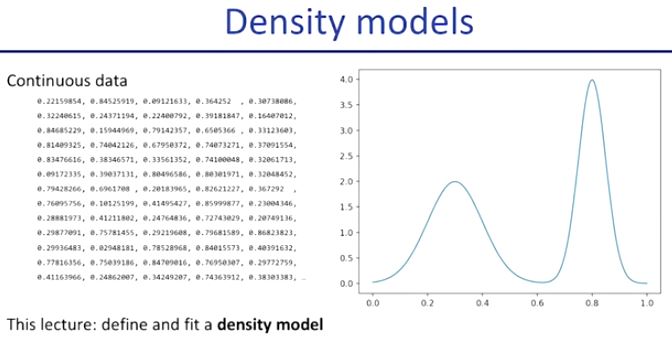
그렇지만 우리는 continous data(연속적인 데이터)를 바로 이용하고 싶다. 이것을 density model이라고 한다.
그 이유는 density function(밀도 함수)을 통해 확률 계산을 하기 때문이다.
이 함수가 하는 일은 어떤 구간의 확률을 해당 구간 그래프의 누적합을 통해 알 수 있게 해 준다. (확률 밀도 함수에 대한 설명인듯)
이 density model과 compatible(호환이 되는)하면서도, train가능한 모델을 찾아야 한다. 이 것이 density model을 디자인 할 때 중요한 포인트가 된다.
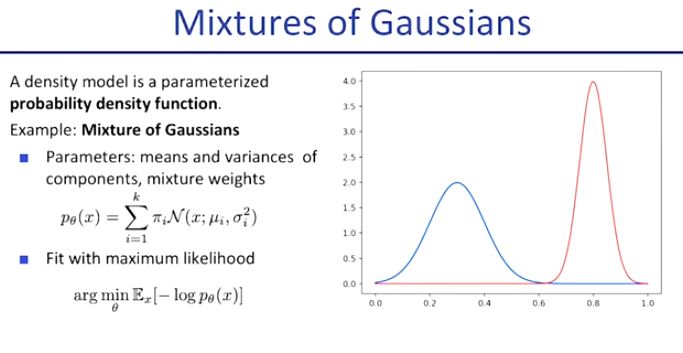
가우시안 density model은 이러한 관점에서 굉장히 전통적이고 많이 사용되었던 모델이다.
Mixtures of gaussians는 말 그대로 가우시안 모델의 총 합이다.
위 그래프의 경우 파란색 가우시안과 빨간색 가우시안의 합으로 새로운 그래프를 만든 예시를 보여주고 있다.
하지만 예상할 수 있듯, 이것은 우리의 최종 모델의 모양은 아니다.

그 이유는 high-dimension data에서 잘 동작하지 않기 때문이다.
Mixtrues of Gaussians 모델로 돌아가서 sample 한다는 의미에 대해서 생각 해 보면, 어떤 gaussian 하나 하나들을 모아서 데이터의 분포를 만들어낸다는 것이다. (또는 gaussian noise를 image에 더해서 표현한다고도 생각할 수 있다.)
이 세팅을 이미지에서 생각해보면, 어떤 평균을 sample해서 분산과 함께 가우시안 분포로서 표현하는 것을 여러번 반복한다.
오른쪽 그림은 왼쪽 그림을 가우시안을 통해 표현한 결과이다. sample이 제대로 이루어지지 않는 것을 볼 수 있으며, 이러한 데이터를 표현함에 있어서 가우시안 mixture 모델은 적합하지 않다는 것을 알 수 있다.
그렇다면 우리는 어떻게 해결할 수 있을까?
우리의 목적은 이러한 shortcoming(결점, 단점)이 없는 density model을 정의하는 것이다. 어떠한 방법을 통해 이 곳에 뉴럴넷을 넣을 것이다. 어떻게 할 수 있을까?
관점을 조금 바꾼다면 가능하다.
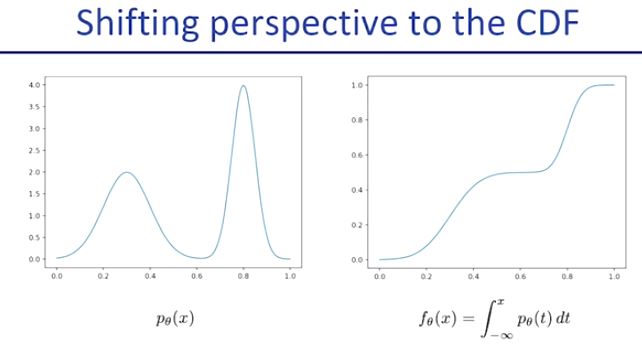
probability density function(PDF)들을 fitting하는 것이 아니라 (즉 데이터에 대한 확률을 맞추도록 하는 것이 아니라) cumulative(누적) distribution function (CDF)을 fitting하도록 할 것이다. (즉 이전에는 위의 그래프 중 왼쪽을 맞추려고 했었다면, 이제는 오른쪽을 맞추려고 한다는 뜻.) 이렇게 바꿀 경우 high-dimensional data를 처리할 때 더욱 유리하다. (자세한 것은 추후 더 설명한다)

CDF function은 invertable(역으로 원래 상태로 돌릴 수 있음)하므로, 위 식의 z(noise의 누적)를 예측하더라도 동시에 x의 값과 p(x)를 예측할 수 있다. (p(x)값은 미분하여 예측이 된다)

우리는 data를 입력받고 그 data distribution을 0과 1 사이의 uniform distribution으로 변환한다.
이것이 invertable하므로 우리는 이 둘이 동일선상에 놓을 수 있다.
예측 모델에 대한 학습이 끝나면 우리는 이 uniform distribution을 예측한 후에 이를 데이터 distribution으로 변환할 수 있다.
이러한 z~x로의 invertable 한 변환, 잠재(latent)변수 등을 통틀어서 flow라고 한다.
확률밀도함수를 근접하게 만들려고 노력하는 것 대신, invertable, differentiable(미분가능)한 neural network를 정의해서 이 invertable한 flow를 직접적으로 이용하기를 원한다.

결국, 우리의 목적은 data를 통해 base distribution이라고 불리는 z(noise)와 mapping 시키는 것이다.
이것이 flow의 최종 목표이다.
그리고 우리가 성공적으로 data를 base distribution으로 mapping 시키는 것에 성공하면, 우리는 new sample들을 model로 부터 생성해낼 수 있다는 말도 된다.

실제 예시이다. after training후의 z 의 distribution을 살펴보면 정규 분포와 닮아있다.

자 그러면 우리는 어떻게 flow를 fitting할까?
우리는 maximum likelihood model을 사용할 것이다.
그렇지만 어떻게 flow를 maximum likelihood model에 맞출 수 있을까?
maximum likekihood 는 probability density에 기반한다. 그렇지만 우리는 더이상 probability density가 아닌 flows에 기반한 모델을 만들어야 한다. 그 말인즉슨, 우리는 어떤 point에 대한 probability density를 flow안에서 계산할 수 있어야 한다는 말이다.
flow는 data에 대한 probability density를 정의한다. 어떻게? 바로 flow의 sampling process를 통해서이다. (z를 뽑아서 f의 inverse를 통해서 x를 구하는 과정)

예를 하나 들어보자.
z ~[0,1]
x = 2z
z = f(x) = 1/2x 라고 하자,
그렇다면 z와 x는 서로 invertable하고 이것을 flow라 할 수 있다.
z가 base distribution이다. (sum of p(z) = 1)
이때, p(x) = uniform[0,2] 인데 p(x)의 총 합도 1이 되어야 하는데 구간의 길이는 2이므로 보정이 필요하다는 것을 알 수 있다. 얼마나 base에서 stretch 되어있는지 알아야 한다.

위의 초록색의 식을 보면 우선 맨 위의 flow라고 표시된 저 식이 위에서 말한 flow이다. (z를 f(x)로 변환해줌)
flow에서 어떤 한 샘플을 뽑는게 어떤 식으로 가능할까?
다시 말해서 x가 [x_0~x_0+dx] 구간이 true인 구간에 도착하려면(임의의 표본이 추출되려면) 어떻게 해야 할까?
우리는 위에 있는 저 아래 P(x ∈ ~~~) 와 P(x)dx 이 같다는 것을 알고있다.
그리고 invertable하기 때문에 이는 또한
P(z ∈ ~~~), 등이 같다는 것을 알고 있다. 그리고 이것은 미분 공식을 생각해볼 때 P(z)f'(x)dx가 된다.

그렇다면 CDF의 flow의 경우는 위의 식 전개와 같다.

위의 왼쪽 그림을 오른쪽과 같은 분포로 만들 함수를 찾는 것. 그리고 오른쪽의 분포로부터 샘플링 한 특정 값으로부터 왼쪽 데이터를 찾는 것이 우리가 할 것임을 명심하자.

그 행동을 우리는 고차원 데이터에서도 진행할 수 있으며, 우리는 f의 역할에 대해서 다음과 같은 직관적인 이해를 할 수 있다.
만약 관찰될 확률이 높은 데이터 x 라면 (예를 들어 사진이라고 하면 이상한 사진보다는 실물을 사진찍은 사진이 더욱 관찰될 확률이 높을 것) z space에서는 더욱 큰 영역을 차지하고 있을 것이라는 것이다.

flow를 학습시키는 것에 대해서 알아보도록 하자.
윗줄의 식은 방금까지 진행한 우리가 변형한 공식에 대한 것이고 tranining은 maximum likelihood를 통해 진행할 것이다.
아랫줄의 식을 보면 맨 마지막의 Jacobian의 determinant를 계산하는것이 심히 빡센것을 알 수 있다.
(D x D 행렬이기 때문에 엄청 느리다.)

flow를 통해 만든 모델은 미분이 비교적 쉽고, 이산적인 모델에 비해 flow가 선호되는 이유이다.
(확실히는 모르겠지만 미분가능하면 back propagation 가능하다는 말 인가?)


만약 데이터 각각에 대해 f를 적용시킨다고 하면, CDF flows나 affine function 들을 elementwise 하게 이용할 수 있다.
Jacobian이 diagonal(대각선만 0이 아님) 해지므로 미분하기가 짱 쉬워진다. (수학적으로 좀 잘 못 따라가겠다 ㅠㅜ)
다만 하나의 함수가 한번에 한 데이터만 처리하고 다른 데이터에 대한 것은 참조하지(고려하지) 못하므로 이것을 해결해야 한다.

RealNVP라고 불리우는 똑똑한 방법이 있다.
우선 variable을 가지고 절반으로 나눈다. (X_L,X_R)
이게 Z로 오면, X_L로 Z_L을 만들고
이로 인해서 바뀐 파라미터들과 함께 X_R 로 Z_R을 만들어서 그 평균을 통해서 미분을 때려준다.
그러면서 결국 반반 나눈 결과가 그러면 다 미분이 가능해진다! (개꿀!)

저 빨간 부분은 신경쓸 필요 없다고 하는데 왜 그런진 모르겠습니다...
억지로 보다가 피를 토하고 말았습니다... 저는 머 모르겠는데 여튼 결론은 아래 식이라고 하더군여...
여튼 아무튼 결과 잘 나온대요... 후반부는 걍 이해 못했습니다... 흑흑...



