투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)

Unsupervised Learning에 대한 또다른 핫한 분야인 Compression에 대해서 알아보도록 하자.

만약 더 공부를 하고 싶다면 위의 링크에 있는 자료를 더 읽어보도록 하자.
자 그러면 Compression은 무엇이고 우리는 왜 Compression에 대해 집중할 필요가 있을까?

예를 들어 메시지, 이미지, 음악 등을 전송할 때 필요한 bit의 수를 줄일 수 있다.
그리고 그 종류는 크게 Lossy 와 lossless compression으로 나뉜다.
lossy는 어느정도의 정보 손실을 허용하는 전송이고 (예를 들자면 이미지의 화질구지라던지..) lossless는 에러를 허용하지 않는 전송을 말한다.
우선 우리는 lossless compression에 집중해보고자 한다.

위의 목록과 같은 압축 기법 / 커뮤니케이션등이 있다.
자 그러면 과연 global하게 모든 데이터의 경우를 다 손실없이 압축할 수 있는 경우가 존재할까?
그것은 유감스럽게도 가능하지 않다.

위의 경우를 보면 증명이 있따...☆
비둘기집의 원리와 비스무리하게 증명한 것 같은데, 일단 중요한 내용은 아니니 넘어가자.
그럼 어떤 데이터를 압축할 수 있을까?

위와같이 경향성이 있는 데이터의 경우 압축이 가능하다.
직관적으로 노란색 픽셀 사이의 한 픽셀을 삭제한다고 한다면, 그 픽셀은 자연스럽게 노란색이라고 예측이 가능 할 것이다.
반면에, 오른쪽과 같이 경향성이 없는 데이터의 경우는 압축이 불가능하다.
즉, 통계적으로 유의미한 패턴이 존재할 경우에는 그것을 이용하여 압축이 가능하다는 것이다.
그렇다면 압축이란 무엇일까?
일단 압축은 오리지널 정보를 다른 정보로 바꾼다.
예를 들어 문자의 경우, 7bit의 (Ascii code)정보로 아스키 테이블에 따라 변환한다.
아스키 코드는 인코딩 디코딩하기 쉬운 편이다. 그치만 이 정보는 항상 7bit로 정보를 표현하기 때문에 효율이 좋지 않다.
우리가 원하는 것은 자주 등장하는 패턴의 경우 짧게, 거의 등장하지 않는 패턴의 경우 길게 만들어서 압축 효율을 좋게 만드는 것이다.
Q : 그렇다면 우리는 어떻게 애매모호함을 피할 수 있을까?
(여기서 애매모호함이란, Cat = 111000 Dog = 111 Cow = 000 이라면 우리는 111000이라는 코드를 DogCow로 해야할지 Cat으로 해야할지 알 수 없다는 것과 같은 문제점이다.)
A : 그 정답은 어떤 한 코드가 다른 코드의 prefix가 되지 않게 하면 된다.
이렇게 하면 절대로 애매모호할 수가 없다. (그렇지만 필수는 아니다.)
Ex 1 : 특별한 Stop문자를 모든 codeword마다 넣어준다. (e.g. Morse부호등이 있지만 낭비가 심하다)
Ex 2 : 보편적인(General) prefix-free code

모스 부호는 긴 소리와 짧은 소리로 이루어졌고, 한 코드가 다른 코드의 prefix일 수 있지만 모든 소리 사이에 묵음이 긴 시간을 넣어주므로 구분할 수 있다.

Prefix-free Codes는 Binary tries 등이 있다.
바이너리 트리를 통해서 0과 1로 트리를 만들고 leaf에 키를 넣는 형식이다.
위의 그림을 참고하여 이해하면 편하다.
이 압축 기법은 트리를 어떻게 구성하느냐에 따라 길이가 변한다. 왼쪽 그림보다 오른쪽 그림이 더 효율적으로 압축한 것을 볼 수 있다.
이 prefix-free code의 최적을 구하는 방법은 이미 존재한다. 바로 Huffman Codes 이다.

입력 받은 symbol i 가 차지하는 비율을 p[i]라고 하자.
그 후 모든 symbol이 하나가 될 때 까지 아래를 반복하면 된다.
1. 최소 비율을 가진 p[k]와 p[l]을 찾자.
2. p[k]와 p[l]을 합쳐준다. (Tree로 따지면 공통 부모로 묶어 0 1 분기를 만들어 준다.
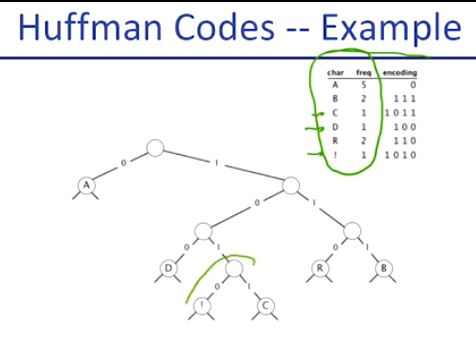
위의 예제와 결과를 보면 이해가 쉬울 것이다.
freq가 가장 낮은 것 부터 차례로 묶어주었다.


그렇게 허프만 코드를 응용한 많은 파일 형식들이 있다.
그렇다면 이제 궁금증이 생길 차례이다. 도대체 이 압축 기법의 한계는 어떤 점에서 오는걸까?
우리가 생각해야 할 점은 symbol들의 패턴이 확률적으로 유의미한 패턴을 가지고 있고, 그렇기 때문에 우리는 그것을 활용해서 더 짧은 string으로 더 많은 확률을 가진 패턴을 대입시키는 것이다. 이 때 우리는 위와같은 접근에서 어떤 한계를 볼 수 있으며 어떻게 해결할 수 있을까?
샤논이 1940년대에 만든 엔트로피라는 개념이 있다.
어떤 데이터가 얼마나 생소하고 자유분방한지에 대한 식인데
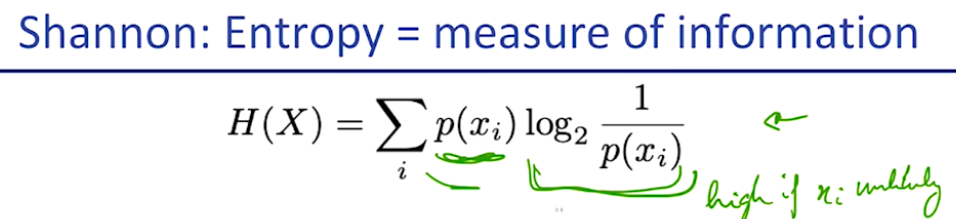
이것은 연속적인 symbol의 분포 X에서
x0~ xn까지 순서대로 이름붙여진 random variable들이 있을 때,
p(x_i) * log_2 (1 / p(x_i) ) 라는 식의 총 합으로 표현된다.
초록색 부분은 해당 단어가 나올 확률이고, 보라색 부분은 생소한 단어일수록 우리가 출현했을 때 놀랄(?) 가능성이 높다라는 의미이다. 그러니까 어떤 단어가 우리를 놀라게 하는 정도를 얼만큼 자주 놀라게 하느냐에 곱한것이라고 볼 수 있다....(....)

이 식이 reasonable한 이유는 왼쪽과 같이 분포도가 자유분방한 상태와 오른쪽과같이 예측이 비교적 가능한 상태일 때 오른쪽의 데이터가 더 낮게 결과를 내보내는 결과를 도출할 수 있는 식이기 때문이다.
우리는 이것을 공부하기 위해서 두개의 부등식(inequality)이 필요하다.
첫 번째로, Kraft-McMillan Inequality는 모든 uniquely decodable code에 대해 (다시말해, 각각에 대해 고유하게 decode가 가능한 코드가 있을 때) 아래의 부등식을 만족한다는 것이다.

(자세한 설명 위키)
https://en.wikipedia.org/wiki/Kraft%E2%80%93McMillan_inequality
s->symbol(예를 들어 알파벳, 문장부호 등)
w->압축된 codeword
C->압축을 풀 수 있는 표
l(w)는 w 라는 code의 길이
식을 조금 직관적으로 살펴보자면 모든 알파벳을 표현할 때에 있어서 l(w)가 길면 길수록 위의 부등식을 만족하기가 편해지는 것을 알 수 있을 것이다. 반대로 말하자면 l(w)를 줄일 수 있는 한계가 존재한다는 뜻이다. (압축한계)
그리고 두번째 식은 아래와 같다.

만약 length들을 모아놓은 L이라는 집합이 있을 경우, 위 식을 만족한다면
prefix code (허프만 코드와 같은) C가 존재한다는 것이다.

식의 증명은 위와 같다. (흐름상 중요한 내용은 아니다)

이제 우리는 샤논의 theorem에 도달했다.
데이터 분포의 엔트로피 H(x)가 모든 상황에서 평균적인(average) 코드(C) 길이(l)보다 작거나 같다는 것이다.
그리고 희망하건데, 더욱 기술을 발전시켜서 평균적인 코드 길이를 엔트로피와 거의 근사하게 만드는 것이 목표인 것이다.

우리가 그 값에 근접할 수 있을까?
위와 같이 증명할 수 있다. 허프만 코드가 optimal prefix code이다. (증명 스킵 ㅠ)

샤넌이 1951년에 영어의 엔트로피를 실험적으로 (설문조사를 통해) 영어의 다음 글자를 예측해보라고 한 후, 그 엔트로피를 구해본 결과 1bit로 한 글자를 압축할 수 있었다고 한다.
우리는 여기에서 고민해봐야 할 것이 있다.
우리가 예측하는 모델의 확률 p_hat 가 잘못될 경우 제대로 구한 p를 통해 추가적인 이득을 볼 수 있을지.
그렇다면 다른 높은 차원의 모델을 통해 더 좋은 확률을 계산할 수 있을지
그리고 추가적인 등등을 통해 아직 성능을 개선할 여지가 많이 남아있다는 것이다.

우리는 KL divergence를 통해 우리가 예측한 p_hat과 p의 차이를 구할 수 있고, 이것을 통해 실제 p를 통해 만들어낸 코드보다 p_hat을 써서 생긴 손해를 표시해줄 수 있다.

만약 P(X)가 이미 높은 entropy를 가지고 있다면 어떻게 추가적으로 압축할 수 있을까?
이 질문에 대한 답은 P(X)만을 가지고 압축을 하는 것이 아니라 Context를 참고하여 P(X|C)를 이용하는 것이다.
예를 들어 이전에 보냈던 데이터들을 알고 있다거나, 이전에 작성된 문서들을 알고있다거나 한다면 그 이후 어떤 데이터가 등장할지에 대한 예측이 훨씬 쉬워 질 것이다.
Autoregressive model은 정확히 그러한 일들을 한다고 볼 수 있다.

우리는 매 심볼 사이에 +1이라는 잠재적인 끊어가는 코드를 필요로 했었는데 Arithmetic Coding을 통해 그것을 피해보려는 시도 또한 있었다.
인덱싱을 분포로 인코딩하는 것이다.

우리가 aaba를 인코딩하고 싶은데 출연 확률이 위와 같다고 하자.
그러면 우리는 출연 확률에 따라서 적당한 비율을 나눠서 첫 글자가 a일 경우 0~0.8에, b일 경우 0.8~1 사이에 위치시키고
첫 글자가 a 인데 두번째 글자가 a일 경우엔 그 사이에서 0~ 0.8*0.8위치 이전에 위치시키고..
하는 식으로 인코딩을 하는 것이다.
더 좁은 영역(더 긴 소숫점)을 표현하기 위해서는 더 긴 bitstream이 필요하므로 위와 같은 방식을 택하는 것이 합리적이라고 할 수 있다.
단 하나의 추가적인 정보가 필요한데, P(a) 와 P(b)만을 맨 처음에 전송하면 된다.

그리고 이것이 Autoregressive Model에 적용될 때면, 위와 같이 조건부 확률을 예측하는 모델이 예측한 p를 통해 좀더 효율적인 공간 분배를 할 수 있게 된다.

Lampel Ziv 알고리즘이다.
압축 관련하여 큰 그림에서 볼 때 참고하기 좋은 알고리즘이다.

별게 없다.
Output Code들을 이용하여 쭉 알려주는데, 지금까지 이전에 보낸 output 중 제일 많이 겹치는 부분을 이어붙이고 마지막에 한 글자를 추가하는 것이다.
(시작위치 (현 위치로부터 마이너스 몇?) , 복붙할 개수, 마지막에 추가할 알파벳)
처음 0 0 a로 첫 a라는 글자를
두번째의 1 1 c로 a를 복사하고 c를 추가하여 aac를 만든다.
다음은 3번째 전으로부터 a a c a를 복사하고 b를 이어붙여서 a a c a a c a b 를 만든 것이다.
... 이런식으로 쭉 인코딩을 한다.
이것이 재미있는 점은 autoregressive model 같이 이전 데이터에 연관지어서 새로운 데이터를 만든다는 것이다.

위 링크에 챌린지가 있다고 한다.



