투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)
이 글은 cs231n보면서 같이 보시면 도움이 되실 것이에오!
유튜부 말구 참고한 링크
https://www.slideshare.net/CurtPark1/dqn-reinforcement-learning-from-basics-to-dqn
https://www.popit.kr/torch-dqn-%EA%B0%95%ED%99%94%ED%95%99%EC%8A%B5-%EC%86%8C%EA%B0%9C/

agent 가 environment와 상호작용하면서 reward를 얻어내는 방식을 구현하려 한다.
목표는 어떻게 하면 reward를 최대화 하는지 공부하는 것이다.

글의 순서는 위와 같다.
RL이 뭔지 배우고, Markov Decision Process에 대해 배우고, RL 알고리즘의 두개의 주된 알고리즘인 Q-Learning과 Policy Gradients를 배울 것이다.
우선 상황 세팅을 먼저 알아보자.
Enviornment는 Agent에게 State s_t 를 줄 것이다. 그 후에 Agent는 상황에 따른 Action a_t를 할 것이다. 그렇다면 그 후에 Acton a_t에 따른 반응으로 Reward r_t와 그 다음 State s_(t+1)을 줄 것이다. ( 그림을 참고하면 더 직관적이다 )
이런 반복을 Enviornment가 종료 state를 전달하기 전까지 반복한다.
상황에 대한 예시를 보자.

이 문제는 막대를 카트의 위로 균형을 맞춰서 잘 세우는 문제이다.
state로는 각, 각속도, 위치, 수평속도가 주어지고 우리가 취할 수 있는 Action으로는 수평으로 주는 힘을 조절 할 수 있다. Reward는 pole이 위를 향하고 있을때 1씩 받게 된다.

이 문제는 로봇을 앞으로 움직이는 문제이다.
State는 각 관절의 각도와 위치이다. 액션은 관절의 토크 적용이고 리워드는 1 time step마다 앞쪽으로 얼마나 갔는지에 대한 정보이다.

위에 있는 Atari 게임들 또한 대표적인 강화학습에 적용 가능한 게임이다.

마지막으로 바둑. 목표는 게임을 이기는 것이고, 상태는 바둑판에 어떤 모양으로 돌들이 존재하느냐 하는 것이며 액션은 다음에 어디에 놓을 것이냐 하는 것이다. 리워드는 이기면 1 아니면 0이다.
자, 그럼 이제 어떻게 RL 문제를 수학적으로 풀어냏 수 있을까? 맨 처음에 그림처럼 state -> action -> reward & state에 대한 것을 한번 풀어보자.

Markov Decision Process(MDP)는 RL 문제에 대한 수학적 수식이다. 마르코프 현재 state특성은 실 생활의 state 특성을 만족시킨다.
MDP는 object 튜플들로 정의되어 있다.
S는 가능한 state이고 A는 가능한 action들, R은 (S,A)에 대한 우리의 reward 분포, P는 전이확률( (state,action)가 주어졌을때 다음 상태에 대한 확률), 감마는 할인 factor 이다. (? 이렇게 해석하는게 맞는지 모르겠다. reward가 금방 얻어지는지 혹은 나중에 얻어지는지에 대해서 얼만큼의 가치를 부여할것인지에 대한 factor이다. 주로 가면 갈수록 리워드의 가치를 줄여서 최대한 일찍 리워드들을 얻어가게 하는 것에 가치를 주는 것이다.)

MDP는 t=0일 때 environment(아마 현재 상태를 구성하는 환경을 말하는 듯)는 initial state 분포로부터 initial state를 샘플링한다.
그리고 그 후 끝날때까지 loop를 도는데
Agent는 action을 select하고
Environment 는 리워드를 샘플하며 또한 다음 state를 샘플한다.
Agent는 리워드와 next state를 입력받는다.
우리는 이를 기반으로 정책 파이를 정의할 수 있는데, 각 state에 어떤 action을 해야 하는지에 대해 정의하는 정책이다.
우리의 목적은 정책 파이* 를 누적 할인된(아까의 그 감마 피쳐에 대한 영향을 적용한) 리워드를 최대한으로 만드는 것이다.
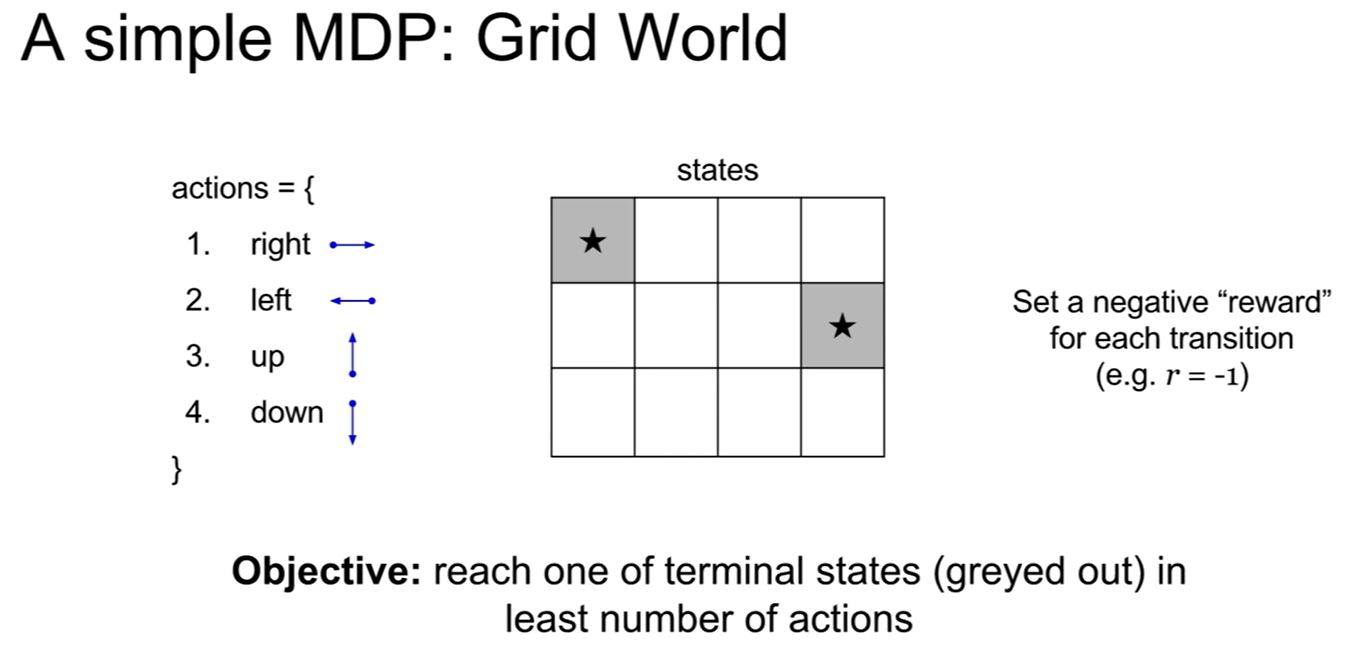
위의 경우를 보자. grid of state가 있다. 이 상태에서 상하좌우로 이동하는 action들을 적용해야 한다. 그리고 우리는 각 시간이 지날 때 마다 -1의 리워드를 얻게 될 것이다. (이동하는게 횟수 소모하는 것이니까)

이 때 랜덤 정책을 가질 때와 optimal 정책을 가질 때는 위와 같이 표현할 수 있겠다.
(Policy란 현재의 상태(state)에 대해 어떤 행동(action)을 할지 결정하는 역할을 한다)
우리는 이제 optimal policy 파이* 를 정의하고싶다. (리워드를 최대로 하는)
이 때, 어떻게 randomness를 다룰 수 있을까? (초기 상태, 전이 확률 ... 등등 다양한 경우의 수가 있겠으니,)
시간이 지남에 따라서 어떻게 이동하는지 등등을 모두 아우를 수 있을까?

이 것을 가능하게 하는 것은 기대되는 reward의 총 합을 최대화 하는 것으로 해결할 수 있다.
물론 이것은 액션과 샘플링을 점점 커지는 t에 대해서 계속 하면서 얻어지는 것이다.

일단 우리의 진행 상황 s_0 a_0 r_0 s_1 a_1 r_1 ... 들이 있다고 해보자.
우리가 얼마나 좋은 state에 있는지는 어떻게 알 수 있을까?
state s 에서의 value function은 state s에 대해서 예상되는 누계 보상으로 정의내릴 수 있다.
(기존의 reward signal보다 장기적인 관점에서의 가치를 의미한다. 어떤 state에 대한 value라고 하면, 그 state를 시작으로 agent가 얻게 되리라고 예상되는 reward의 총합이라고 할 수 있다.)
그렇다면 state - action pair (즉 어떤 상태 s에서 a를 행동했을 때) 은 어떻게 평가할 수 있을까?
이것 또한 마찬가지로 예상되는 누계 보상으로 정의내릴 수 있다.
위의 경우를 Value f, 아래의 경우를 Q-value f 라고 한다.

최적화된 Q value function 인 Q*은 (state , action) 쌍에 대해 최대로 기대되는 누적 보상을 내야한다.
이제 RL에서 중요한 식 중 하나인 벨만 식을 알아보자.
Q중, 최적화된 정책 Q*에 대해 생각해보자.
이것은 벨만 식을 만족하고
그 벨만 식이라고 하는 것은 s랑 a의 스테이트가 주어졌을 때, 얻게 되는 reward r + 그 후에 얻게되는 state 에 대한 value 이다.
우리가 optimal 한 policy 를 가졌다고 가정하면 우리는 우리가 할 수 있는 것 중 최선의 action으로 play할 수 있다는 것을 알 것이다. 그렇게 되면 결국 Q를 통해 쭉쭉 넘어가는 시간에 대해 최적을 구할 수 있게 된다.
최적의 정책 파이*는 Q*에 특정되어진 최적의 action을 취하는 것에 연관되어 있다.

그렇다면 어떻게 이걸 풀 수 있을까?
-> value iteration algorithm : bellman equation을 iterative update에 사용하자.
매 스텝마다 우리는 bellman equation을 최적화하기 위해 Q*로부터 나온 우리의 approximation을 개선할것이다.
그렇지만 여기에서의 문제점은 우리는 모든 pair s,a에 대해 최적화를 진행하기에는 너무 경우의 수가 많다는 것이다.
이 해결책은 Q(s,a)를 어림잡아 측정하는 function approximator을 사용해서 계산하는 것이다. (뉴럴 넷 같은걸루!~)

우리의 action value function 을 approximate하기 위해 deep learning을 사용할 때 deep q-learning이라고 한다.
(즉 말은 거창하게 했지만 최적의 action을 구하기 위한 파라미터 세타를 구하는 딥러닝을 만들겠다는 뜻이고, 저 위의 수학적으로 예쁜 식을 통해 loss function을 가져가겠다는 뜻인 것 같아요 홍홍)
-> 추정이 action value 에 최대한 가까워진다면 객관적으로 좋은 행동을 선택할 수 있으리라 기대할 수 있게 된다.
Greedy actions : 매 시도에서 Q함수의 값이 가장 높은 action들의 집합
Exploiting : Greedy actions중 한가지 action을 선택하는 것.
Exploring : non-greedy actions중 한가지 action을 선택하는 것.

자 이제 functional approximation이 주어졌을 때, 우리는 어떻게 우리의 최적화된 정책을 찾을까?
일단 Q-function 은 bellman equation을 만족한다는 것을 기억하자.
우리는 bellman equation이 일어나게 하고 싶은 것이다. (최적화된 step만을 반복하는 것)
우리가 이 Q-function을 예측하는 뉴럴넷을 가지고 있을 때, 우리는 우리의 loss function이 bellman equation으로부터 에러를 최소화 하는 방향으로 설정함으로써 Q-function을 학습할 수 있다.
우리의 목표는 Q-value를 target value(y_i) 와 근접하게 만드는 것이다.

case study를 해 보자.
Atari game을 할 때, 우리의 목적은 최대 score을 먹는것이고, 각 timestep에 대한 보상은 점수가 증가하거나 감소하는 것에 대해 준다면 될 것이다.

실질적인 네트워크 구조는 다음과 같을 것이다.
파라미터 세타를 가지는 Q 네트워크는 위 그림과 같다.
input state s_t의 경우 preprocessing( rgb->grayscale conversion / downsampling / cropping )을 한 후에 남은 최근의 84x84의 4 개의 frame 정보가 남아있다.
네트워크 자체는 단순하다. 마지막 FC layer은 4d의 아웃풋을 가진다(만약 상하좌우에 대한 4개의 action들만 있다면).
이 action 각각은 Q(s_t,a_1) , Q(s_t,a_2) , Q(s_t,a_3) , Q(s_t,a_4) 이다. (atari game의 종류에 따라 4개가 아니라 18개까지 될 수도 있다)
이 네트워크 스트럭쳐에서 굉장히 다행인 점은 현재 상태로부터 단 한번의 feed-forward를 통해 모든 Q-values 함수에 대해 구할 수 있다는 것이다. (바로 결과가 나오니까)

이 것을 학습하기 위해 앞에서 말한 loss function을 통해 backward pass를 진행해주도록 한다.
위의 y_i가 앞서 살펴본 벨만 방정식이다.

이런 글도 잇더라.

Experience Replay라는 것에 대해 다뤄보자.
우선, 연속된 sample들에 대한 batch들로부터 학습하는 것은 문제가 있다.
=> sample들은 서로 연관되어 있다. -> 비효율적인 학습
=> 현재 상태의 Q-network 파라미터가 다음 상태를 sample하는 것을 결정한다. (예를 들어 지금 왼쪽으로 가는게 최적이라고 생각했다면 그 후에는 왼쪽에서 얻은 sample들만 가지고 학습을 진행하게 된다)
이 문제를 experience replay 를 통해 해결하자
=> 게임 에피소드가 play 됨에 따라서 상호작용 테이블 (s_t,a_t,_r_t,s_(t+1)) 메모리를 지속적으로 리플레이 하면서 업데이트 하자.
=> 연속적인 sample들 대신에 replay memory로부터의 상호작용들의 랜덤한 미니배치로 Q-network를 학습하자.
이를 통한 이점.
1. 우선 위에서 발행하는 문제점들을 해결할 수 있다.
2. 하나의 샘플이 가중치 업데이트에 여러번 기여할 수 있다. (여러번 메모리에서 랜덤한 미니배치를 뽑기 때문에)

처음 강의를 들을 때는 이 내용이 명확하지 않았다. (강의의 수도 코드를 봤음에도)
그래서 위의 수도 코드를 첨부한다.

여기까지의 Q learning에는 문제가 있다.
Q-learning 모델이 굉장히 복잡하다는 문제가 있다.
(우리는 (state,action) 쌍에 대해 모두 학습해야 하는 상황이다. 그리고 이것은 아주 어려운 문제가 된다.)
이 것을 policy(정책)을 훨씬 간단하게 정의 할 경우 가능 하게 할 수 있다. (예를 들어 관절을 어떻게 움직여서 무엇을 잡고 어쩌고 저쩌고보다, 단순하게 손을 오무립시다 란 식으로)
그렇다면 여기서 우리는 정책 자체를 바로 학습하는 것이 가능할까?
그렇다면 가능한 정책들 중에 그 최선의 정책 세트를 찾는 것이 가능할 것이다.
정책을 결정하기에 앞서서 Q-value를 추정하는 과정을 거치지 않고 말이다.

이러한 접근이 policy gradients다
일단 파라미터화된 정책들의 클래스들을 정의한다.
정책들은 세타라는 가중치에 의해 매개변수화 된다.
각 정책에 대해서 그 보상 값을 위의 J(세타)의 식으로 정의하자.
저 식의 경우 기존에 가지고 있던 리워드 함수와 비슷하다. 이를 통해 J(세타)를 최대화하는 세타*를 찾자.
그리고 gradient ascent를 통해서 세타*를 구할 수 있다.

정책의 정의에 대한 관련 슬라이드 사진을 첨부한다.

좀더 자세하게 알아보자
위에 Reinforce 알고리즘이라고 하는 알고리즘이 있다.
수학적으로, J(세타)를 궤적(trajectory)에 대한 미래 보상의 기댓값으로 나타낼 수 있다.
즉, 세타라는 정책에 대한 얻어지는 궤적에 대한 최종 보상을 J(세타)라고 놓는 것이다.
이를 위해서 궤적을 샘플링해야한다. (s0 ,a0, r0, s1, a1, r1, ..... ) 같은 것이 예가 될 수 있겠다.
이 궤적은 궤적 파이_세타에 의해 결정된 것이다.
그러면 각 경로에 대해서 보상을 계산할 수 있다. (우리가 어떤 경로를 따라 얻을 수 있는 누적 보상이 될 것이다)
따라서 정책인 파이_세타의 값은 샘플링 된 경로로부터 받게 될 보상의 기댓값이 될 것이다.
우리는 저 궤적(trajectory)의 보상을 r(타우)라고 한다. (타우는 궤적,경로 를 의미한다)

gradient ascent를 해야 하니 한번 미분 해 보자. 예상된 기대값은 맨 위와 같다.
그렇지만 식을 저 상태에서 미분할 경우에 gradient가 흐르지 않는다. 왜냐하면 p가 세타에 의존하기 때문이다. tau에 대한 적분을 수행해야 하기 때문이다. 그렇지만 이걸 트릭으로 해결해내버린다.
위의 맨 아래 식으로 변형해서 쓸 수 있다.
이 트릭은 p를 가지고 하는 것인데, 어차피 1을 곱하면 그대로이기 때문에 위아래에 p(타우;세타)를 곱해준다.
그러면 2번째 3번째 수식이 같은데, 이유는
이 수식 때문이다.

여튼 식이 기댓값에 대한 기울기를 계산하는 것이었는데
이것을 기울기에 대한 기댓값으로 바꿔버렸다고 한다.;;;
이로 인해, 기울기를 추정하기 위해 경로를 샘플링해서 사용할 수 있게 되었다.
따라서 이제 몬테카를로 샘플링을 통해 추정하는 것으로 해결할 수 있다고 한다.... 이게 주요 아이디어라는데 잘 모르겠다.
https://www.slideshare.net/DongMinLee32/part-2-91522217
https://www.slideshare.net/WoongwonLee/rlcode-a3c
잘 모르겠어서 다른 슬라이드 찾아봤다. 아래 링크 슬라이드에 관련 내용이 나온다.

p(타우;세타)는 t=0으로부터 전이확률과 발생확률을 쭉 곱한것이고,
따라서 로그를 씌우믄 그 아랫줄처럼 된다.
우리가 미분을 할 때, 세번째줄에는 전이 확률은 필요 없다. 왜냐하면 세타에 의존하지 않는 식이기 때문이다.
따라서 우리는 어떠한 경로 타우에 대해서도 기울기를 기반으로 J(세타)를 추정해 낼 수 있다.
https://www.popit.kr/torch-dqn-%EA%B0%95%ED%99%94%ED%95%99%EC%8A%B5-%EC%86%8C%EA%B0%9C/
위 링크 보고 수식적이지는 않은 부분들을 대충 이해 했다.
위 슬라이드가 말하고 싶은건 결국 J(세타) 미분한 값은 저 시그마 머시기 친구로 대략적으로 수렴된다는 것이다.
+ 결국 우리는 샘플링을 하게 되며, 기댓값을 계산하기 위해 여러개의 경로를 샘플링 할 수도 있을 것이다.

이제 이 reward 측정기 J가 생겼기 때문에 우리가 하고 싶은건, r(타우)가 높을 경우에 관찰된 행동의 확률을 높이고, r(타우)가 낮을 경우에는 관찰된 행동의 확률을 낮출 것이다. (즉 잘한 행동의 발생 확률은 높이고 못한 행동의 발생 확률은 낮출 것이다)
(likelihood 는 x를 가지고 x의 함수를 추정하는거.....라고 쉬발!!!!!!!!!!!!)
아마 쉽게 생각해서는 궤적(경로)이 좋을 경우에는 그 모든 action들이 좋았다고 평가받을 것처럼 보인다. (그니까 안좋은 행동들까지도 좋은 것 처럼 여겨지는?) 그치만 기댓값에 의해서, 그것은 평균화 되어버린다.
그러나 여기의 문제는 분산이 너무 높다는 데에 있다. 신뢰할당문제?(credit assignment)가 아주 어렵기 때문이다. 일단 보상을 받았으면 해당 경로의 모든 행동들이 좋았다고 평가 받을텐데, 구체적으로 어떤 행동이 최선이었는지를 알아낼 수 있기 보다는 모든 정보가 평균화 되어 버리는 바람에 어떤 행동이 특히 좋았는지 등은 알 수 없다.
좋은 평가를 위해서는 충분한 샘플링밖에 답이 없다.

Variance reduction은 policy gradient에서 굉장히 중요하다.
적은 샘플링으로 estimator을 개선할 수 있기 때문이다.
첫 아이디어는 해당 상태로부터 받을 미래의 보상만을 고려하여 어떤 행동을 취할 행동을 키워주는 것이다.
해당 경로에서 얻을 수 있는 모든 보상을 고려하는 것 대신에 현재의 time step부터 미래의 time step만을 가지고 J(세타)를 계산한다. 이를 통해 어떤 행동이 발생시키는 미래의 보상이 얼마나 큰지를 고려하겠다는 의도를 줄 수 있다.
두번째 아이디어는 지연된 보상에 대해서 할인율을 적용하는 것이다.
당장 받을 수 있는 보상과 조금 더 늦게 받은 보상간의 차이를 구하는 것이다.
어떤 행동이 좋은 행동인지 아닌지를 해당 행동의 가까운 곳에서 찾는다.
(다만 먼 미래에서 스노우볼링 된 행동에 대한 평가는 잘 하지 못할 것이다)


두 방법을 적용한 reinforce 알고리즘 업데이트 식에 대한 슬라이드이다. 위에 있던 링크에서 가져왔다.

세 번째 방법은 베이스라인을 정하는 것이다.
위 수식에서는 b(s)함수로 표현되어 있는데, 가령 항상 포인트가 양수인 어떤 게임을 생각해 보았을 때, 우리는 항상 모든 약션에 대한 확률을 끌어올리기만 할 것이다. 그렇다면 올바른 행동만 남기는 데에 차질을 겪을 것이고 이것을 해결하기 위해서 어떤 state에 대해 기대되는 baseline을 계산하는 함수를 만들어서 그것을 빼주도록 하자. 그러면 어떤 행동이 우리가 기대한 값보다 상대적으로 큰지 작은지에 대해서 알 수 있게 된다.

어떻게 베이스라인을 구할까?
가장 단순한 베이스라인은 지금까지 경험한 보상들에 대해서 average를 구하는 것이다.
에피소드를 수행하는 학습 과정에서 지금까지 봤던 모든 경로들에 대해 보상이 어땠는지 평균을 구하는 것.
지금까지 배운 variance reduction 방법을 통상적으로 vanilla REINFORCE 라고 부른다.

어떻게 베이스라인을 정할 수 있을까?
더 좋은 베이스라인은 내가 어떤 state로부터 받을 수 있는 기대 보상 값을 가져야 맞다.
그렇다면 그것은 앞서 언급한 value function과 기능이 같다.
그를 통해서 우리는 estimator을 위의 Q - V에 대한 식으로 구할 수 있고, 마찬가지로 J도 Q와 V에 대한 식으로 표현할 수 있게 된다.

REINFORCE 알고리즘에서는 Q와 V를 구하지 않았는데, 이를 어떻게 학습시킬 수 있을까?
우리는 policy gradient와 Q learning을 동시에 사용하여 학습시킬 수 있다.
여기에서는 actor가 policy이며 critic이 Q-function이 된다.
이들은 어떤 상태가 얼마나 좋은지, 그리고 상태에서의 어떤 행동이 얼마나 좋았는지를 말해준다.
Actor-Critic Algorithm
에서는
actor은 어떤 행동을 취할지를 결정한다.
critic(Q-function)은 그 행동이 얼마나 좋았으며, 어떤 식으로 조절 해 나가야 하는지를 알려준다.
(?? GAN이랑 비슷하네)
단 Q function은 기존에는 모든 (s,a)쌍에 대한 Q-value를 학습해야 했지만 여기에서는 policy가 만들어낸 (상태,행동) 쌍에 대해서만 학습을 시키면 된다.
자, 이제부터는 Q(s,a) - V(s)가 보상 함수가 될 것이다. 보상함수는 어떤 행동을 했을 때 얼마나 많은 보상이 주어지는지를 나타낸다. (행동이 예상했던 것 보다 얼마나 더 좋은 것인지를 나타내는 것)

알고리즘의 순서도이다.
우선 정책 파라미터 세타랑 평가 파라미터 파이를 놓는다.
그 후 매 이터레이션마다 현재의 정책 아래에서 m개의 궤적을 뽑는다.
그 후 m개의 궤적들에 대해서 보상 함수를 계산한다.
그리고 그 보상 함수를 이용해서 gradient estimator을 계산하고 전부 누적시킨다.
또한 평가 파라미터인 파이 또한 학습시켜야 한다.
이를 위해선 가치 함수를 학습시켜야 하는데 잇는 보상 함수를 최소화시키는것과 동치이다.
이를 통해 가치 함수가 벨만 방정식에 근사하게 할 수 있다.
활용을 아래와 같은 방법으로 하기도 한다.

저해상도 이미지를 대충 보고 중요한 부분에 대해 더욱 집중하여 다시 볼 수 있도록 한 것임.
state 는 지금까지 관찰한 glimpses(흘끗 한번 본, 여기서는 작은 사각형)이다.
action은 다음에 이미지 내에 어떤 부분을 볼 지 선택하는 것
실제로는 다음 스텝에서 보고싶은 고정된 사이즈의 glimpse의 중간 x-y좌표가 될 수 있음.
reward는 이미지가 제대로 학습 되면 마지막에 1을 주고 아니면 0을 준다.
이 glimpses에서 강화학습이 필요한 이유는 glimpses를 뽑아내는 것은 미분이 불가능한 연산이기 때문이다.
그래서 이 정책을 reinforce로 학습시키는 것이다.
우리의 코어 모델은 RNN이며, 우리는 policy 파라미터를 통해 다음 action을 측정하도록 할 것이다.

이 모델은 input 이미지를 받아서 glimpse를 얻어내고 (그림의 빨간 박스) 이 glimpse를 입력으로 받아서 뉴럴 넷을 통과시킨 후 다시 볼 x y를 뽑아내는 과정을 반복한다.
다만 이 과정에서 임의의 반복 횟수를 정해놓는다. (6번, 8번 등의 반복)
그리고 그 마지막에 softmax를 하여 2라는 정답을 얻어낸다.
이 상태에서 softmax의 결과로부터 경로를 샘플링하고 기울기를 계산해서 backprop을 진행한다고 한다.
(구체적으로 수식은 잘 상상이 안간다. 그냥 RNN 하듯 하는게 아니라 경로를 샘플링 하는 과정이라면
어떤 파라미터에 얼만큼의 loss가 걸리는지를 전부 저장하는건가? 아니면 그저 softmax 후에 정답을 1로 만들고 일치하면 1 아니면 0이라고 해서 그저~ 리워드를 1 0 으로 주는건가? <-는 이게 정답같네)
이 Hard attention이라는 아이디어는 수년간 이용되어왔다.
이미지의 불필요한 부분을 무시할 수 있기 때문에 계산 효율이 좋다는 점이 좋은 점이다.

이제 그 알파고다.
역시 policy gradients를 사용.
supervised learning과 reinforce learning을 같이 사용하였다.
몬테카를로 tree search 와 등등 다 사용
우선 입력 벡터를 만든다.
board의 feature를 만들어서 그것을 입력으로 받는다.
등등 다양한 규칙들을 정의하고 나면 프로 바둑기사의 기보를 가지고 supervised mapping을 통해 학습 한다.
그리고 그 후 policy network를 학습시킨다. (action을 정해줌)
알파고는 임의의 자신의 이전 대국과 대국을 둬서 이기면 보상을 받고 지면 -1의 보상을 받는다.
최종적인 알파고는 policy/value network와 monte carlo tree search 알고리즘의 결합된 형태이다.
알파고의 다음 착수는 value function과 MCTS(몬테카를로트리서치)로 계산된 값의 조합으로 결정한다고 한다.

서머리
gradient descent / ascent 를 통한 policy gradients를 배웠다.
Q-learning 을 배웠다.
Policy Gradients 는 J(세타)를 통해 local minima루 수렴 가능
Q-learning 짱짱
졸업논문땜에 정신이 읍다... 죽겟다 나 우러ㅓㅓㅓㅓㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜ

