투명한 기부를 하고싶다면 이 링크로 와보세요! 🥰 (클릭!)
바이낸스(₿) 수수료 평생 20% 할인받는 링크로 가입하기! 🔥 (클릭!)

기존 강의는 pixelCNN의 설명부터 시작한다.
VAE는 intractable한 (조절이 까다로운?) latent(잠재) vector z에 대한 density function을 알아내려 한다.
다만 바로 직접적으로 모델을 학습시킬 수는 없고, 대신 likelihood 의 lower bound를 derive and optimize한다고 써있는데 아래에서 더 자세히 알아보도록 하자.
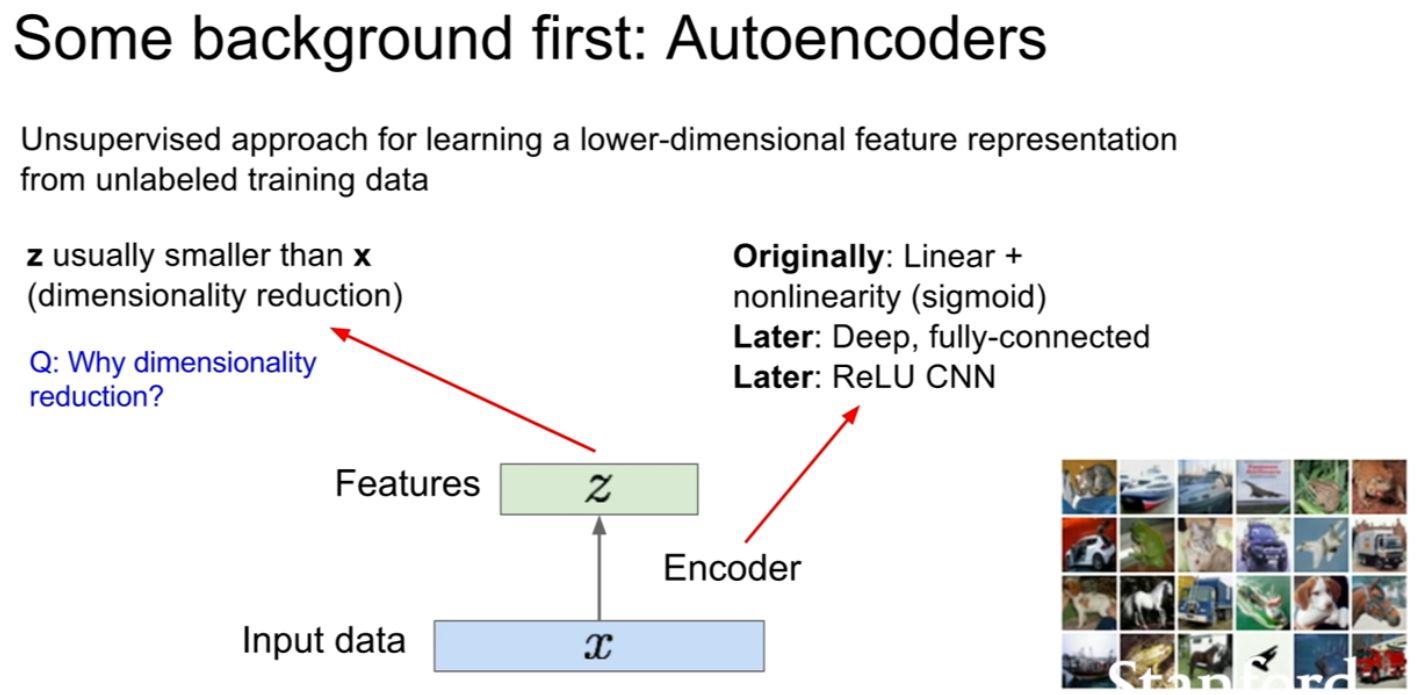
우선 VAE의 배경이 되는 Autoencoder는 data를 만들어내기 위하여 사용하지 않고, label 되어있지 않은 트레이닝 데이터로부터 lower dimensional feature을 unsupervised learning을 통해 배운다.
input data x가 있고 이 데이터로부터 feature z를 생성하도록 Encoder을 학습시킬 것이다.
원래의 인코더는 linear + nonlinearity를 통해서 설계되었고 그 후 Deep, fc 모델을 통해서, 그리고 그 후에는 ReLU CNN을 통해서 설계되어 왔다.
주로, z는 x보다 dimensionality가 축소된다. 그 이유는 z는 x로부터 뽑힌 가장 중요한 정보들만을 담고 있어야 하기 때문이다.

이 autoencoder을 학습시키는 방법은 x를 통해 x를 복원하는 방법을 사용한다.
주로 이 모델은 conv를 이용해서 설계한다.
그냥 데이터만 복구시키면 의미있는 feature들만 남는 이유는 무엇일까?
바로 손실된 적은 양의 정보(z)를 통해서 원본을 복구하기 위해서 의미있는 feature만 남기기 때문이다.
이제 마지막으로 훈련이 끝나면 디코더를 삭제하면 의미있는 feature들을 만들어내는 decoder이 완성된다.

이 encoder로부터 나온 데이터를 feature로 추가적인 모델을 붙여서 classifier의 전처리로 사용할 수도 있다.
좋은 feature을 뽑기 때문이다.

VAE의 경우 우리의 트레이닝 데이터가 latent 한(관찰 불가능한) z 로부터 생성되었다고 생각한다. (기존 아이디어를 거꾸로 뒤집음)
z는 어떤 벡터이고, 각 z는 우리의 training data의 다양한 feature 나타내고 있다고 보자.
자 이제 우리 새로운 generation process로써, z 이전 단계에서 z를 sample 할 것이다. (강의에선 prior이라고 한다)
다시말해서 z의 분포가 어떻게 되어있는지에 대한 Z에 대한 prior을 정할 것이고, 이 prior은 가우시안 등이 될 수 있다.
그후 우리는 조건부 확률 p(x|z)를 통해 x를 만들것이다.

우리는 이 (가우시안 등으로 된 simple한) p(z)를 통해서 p(x|z)를 통해 이미지를 만들어낼 것이다. 이건 복잡하니까 뉴럴 네트워크로 만들게 된다. 이걸 디코더 네트워크라고 하자.
(p(z)를 가우시안이라고 일단 정해보자)

어떻게 학습시킬 수 있을까?
일단 우리가 하려는게 training data같은 데이터가 복원이 잘 되게 하는 모델 파라미터를 학습하는 것임을 기억하자.
일단, p(x) 를 z에 대한 적분 식으로 표현할 수 있다. 그렇지만 그 과정이 구현이 되지 않는다.

p(z)는 simple한 가우시안으로 정했고 그렇기에 얻어낼 수 있다.
또한 p(x|z) 는 디코더 네트워크이기 때문에 연산이 가능하다.
그렇지만 저 적분기호(인터그랄)를 처리할 수가 없다.

또한 베이즈 룰을 통해서 변형한 posterior density 또한 구할 수가 없다.

그래서 우리는 그 대안으로 추가적인 인코딩 네트워크 q(z|x)를 정의해서 p(z|x)를 알아내도록 (샘플링하도록) 하자!

VAE의 경우
인코더는 x를 입력으로 받아서 z|x의 mean 과 (대각 행렬의) covariance 를 구하려고 한다.
디코더는 z를 입력으로 받아서 x|z의 mean과 covariance를 구하려고 한다.

이걸 봐서는 잘 이해가 안간다. (난 강의 들으면서 여기서 약간 설명이 이해가 안갔다)
그래서 다른 (내가 이해한대로) 설명을 덧붙이겠다.
지금까지의 내용 정리를 하자면 우리는 이상적인 z의 확률 분포를 모르기 때문에 임의의 가우시안 분포에서 z를 샘플링 하기로 했다.
그걸 처리하려고 만들어진 모델이 q라고 하자. 결국 q(z|x)는 p(z|x)와 근사한 가우시안을 구하는 역할이다.
그리고 z를 알았다면 x는 p(x|z)를 수행하는 디코더 네트워크를 통해 샘플링 할 수 있게 된다.
그리고 이것을 maximum likelihood estimation 을 통해 최적화 한다.
아래에 그 식 전개를 소개한다.

우선 첫줄, z에 관련없으니 그냥 저렇게 바꿀 수 있다.
베이즈 룰을 이용하여 두번째 줄로 만든다.
셋째줄에 위아래에 같은 q 관련 값을 곱한다. (추후의 식 처리를 편하게 하기 위해서)
넷째줄에서는 그 값들을 세 부분으로 나눈다. (log니까 더할 수 있다 당연히도)
마지막엔 이걸 정리하는데,
첫 번째 항은 디코더 네트워크를 통해 p(x|z)를 계산 가능하다.
저 영어로 써있는 differentiable through reparam이라고 되어있는 (무책임하게 see paper이라고 되어있어서 빡치는) 부분에 대한 설명은, 그냥 일반적인 방식으로 sampling을 하면 중간에 chain rule이 끊겨서 gradient 를 구할 수가 없으니까 다른 방법을 쓰자는 것이다. 그 트릭이랄게, 별로 특별할 것도 없는데
임의의 정규분포 N(0,1)로부터 상수 a를 샘플링 한다.
그리고 기존의 우리가 구한 변수 (평균 + a*분산^2) 을 통해 backprop을 가능하게 하자는 것.
(실제로 수식적으로 같은 표준편차의 그것이 뽑히며, 변수의 값이 직접 조작되지 않았으니 gradient descent가 가능)
두번째 term은 뭐라는지 잘 모르겠다; 알려주실분? ㅜㅜㅜㅜㅜㅜ
세번째 term은 계산할 수는 없지만 0보다 크다는 것은 항상 자명하다.

여튼 결국 이를 통해 lower bound를 추적할 수 있다고 한다. (맨 오른쪽 term도 0 이상이니 왼쪽 두 항을 최소로!)
p(x|z)랑 KL divergence term이 미분이 가능하니까 backprop이 가능하다.

그래서 위의 lower bound를 알게 되었기 때문에 우리는 저 lowerbound를 최대화 함을 통해서 확률 p를 최대한 높일 것이다.
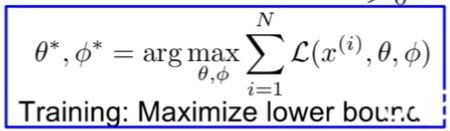

왼쪽 term에 대한 직관적인 해석은 z로부터 최대한 말 되는 x를 뽑아내라 하는 것이다.
z를 보고 최대한 reconstruction 잘 하라는 것.
오른쪽 trem은 저 KL을 최대한 작게 만들라는 것이다.
다시말해 q(z|x)와 p(z)를 최대한 일치하게 만들라는 것.
다시말해 x를 통해 인코딩 될법한 z를 잘 뽑아라.

매 minibatch 마다 forward pass를 진행하고 backprop을 진행하자.
(그 과정에서 우리가 만든 x->z를 원본 z랑 최대한 맞추려고 하고, x 는 생성된 x와 최대한 맞추려고 하면 됨니다.)
이렇게 VAE를 모두 만들었다면,

디코더 네트워크만 가지고서 데이터를 만들어 낼 수 있다.
( ? 이럴거면 왜 training시에 인코더 네트워크를 다시 만든거임? 이라는 생각이 든다. 그치만 다양한 z 분포에 대해 합리적으로 x를 재 생성하게 했으니 다양한 분포를 견딜 수 있는 디코더를 만들게 된 것이 의미라면 의미겠지....?)
여기서 약간 의문인 점이 다른 곳의 포스팅들을 봤을 때는 안 그런데 cs231n의 디코더 슬라이드에서만 마치 동일한 z에 대해서 다른 x를 생성하는 것 처럼 설명 해 놓았다.
왜 z로부터 다시 x를 샘플링하는거지? 그냥 디코딩 하는게 아니라?
그래서 인터넷에서 찾은 VAE 코드 링크를 첨부한다.
아무리 봐도 디코더에서 다시 샘플링 하는건 아닌 것 같다.
https://github.com/lyeoni/pytorch-mnist-VAE/blob/master/pytorch-mnist-VAE.ipynb
그리고 예쁜 설명 동영상이 있다.
https://www.youtube.com/watch?v=9zKuYvjFFS8
참고하면 좋을 것 같다.
(근데 여기서 마지막으로 설명하는 disentangled variational autoencoders 에 대한 설명 자료를 찾을 수가 없다.. 이런..)
(Wasserstein Auto-Encoder도 나중에 공부해보면 좋을 것 같다)
혹시 읽다가 잘못된 부분을 발견하셨으면 제보좀 부탁드립니다........
뭔가 공부 다 했는데 찝찝하다....

