t-score 에 관하여 밑바닥부터 설명

t-점수는 통계적 유의성을 판단하기 위해 든든국밥처럼 자주 소개되는 점수이다.

헷갈리지 않도록 완전 밑바닥부터 다시 차근차근 설명해보는 글을 써보려 한다.

0. 들어가기 전에

• 데이터(Data): 우리가 관찰·측정한 값들의 집합
• 모집단(Population): 관심 있는 전체 대상
• 표본(Sample): 모집단에서 뽑은 일부 데이터

1. 평균(Mean)

​

• 모든 데이터를 더해 개수 n으로 나눈 값.
• “중심”을 대표하는 가장 기본적인 요약값.

2. 분산(Variance)과 표준편차(Standard Deviation)

2-1. 데이터가 흩어진 정도를 어떻게 재나?

각 데이터가 평균에서 얼마나 떨어졌는지(편차, deviation)를 제곱해 평균을 내면 분산이 된다.

• 단위가 ‘제곱’이라 직관이 어렵다 → 제곱근을 취해 표준편차 σ 를 구한다.

​

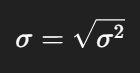
“평균에서 ±표준편차” 범위에 데이터가 얼마나 몰려 있는지가 곧 흩어짐(Dispersion)의 크기이다.

 

2-2. 표본만 있을 때: Bessel 보정

모집단 전부가 아니라 샘플 x1,…,xn ​만 있으면 모평균 μ 대신

를 넣는다.

(기본으로 제공되는 수식 에디터가 없네요.. 눈물..)

 

 

아까 위에서 데이터를 기반으로 구한 평균이 이것이고, 모집단 전체의 평균인 모평균은 μ로 표현하는 것.

 

 

이때 그대로 나누면(분모 n) 약간 작게 추정되는 경향이 있어서, 자유도 1을 빼 n−1 로 나누어 보정한다.

 

 

• s는 σ의 불편(unbiased) 추정량.(즉,편향되지않은,  σ를 추정하는 값)
  • 불편추정량에 대한 위키
• n−1을 ‘Bessel 보정(Bessel’s correction)’이라고 부른다.

처음에는 띠용? 할 수 있다. 아래 링크를 보면 예시가 나오는데, 모집단에서 구한 모평균은 실제의 표본평균을 사용했을 때 보다 늘 분산을 크게 만든다.
베셀 보정 위키

 

정리하자면, s는 σ 를 모집단으로부터 추정한 값이라고 할 수 있다.

 

3. 표본평균의 표준오차(Standard Error, SE)

표본평균

도 뽑을 때마다 달라지는 랜덤 변수다. 그 흩어짐을 나타내는 값을 표준오차(SE) 라고 한다.

 

​

• 표본이 커질수록(√n 분모) 평균 추정이 정확해진다.
• σ를 모르면 대신 s를 넣어 ​  로 추정.

(그냥 데이터가 많을수록 표본평균도 진짜 값에 가깝게 구해져간다는 의미의 식이다.. 정도로 생각하면 편하다.)

 

4. z-점수(z-statistic) ― 모표준편차 σ를 아는 이상적 상황

​​

• ​ : 귀무가설상 모평균 (즉, 우리가 참이라고 여길 모평균)
• 분자가 “관측된 평균-모평균”, 분모가 표준오차.
• σ를 안다는 가정하에 표준정규분포(평균 0, 분산 1)를 따른다.

귀무가설을 잘 모른다면 위키
귀무가설 / 대립가설 / 가설검정 네이버 포스트

 

 

5. t-점수(t-statistic) ― 현실에서 σ를 모를 때

현실적으로 σ 는 거의 항상 미지수다.
따라서 모른 채로 z-통계량을 쓰면 ‘낙관적(꼬리가 얇음)’ 판정이 된다. (그래프 모양이 가운데가 낮고 꼬리가 길다) 이를 교정하기 위해 Student(고셋, 1908) 가 발견한 분포가 t 분포.

• 분자는 동일, 분모는 s (표본표준편차).
• 이 비율은 t 분포를 따르는데, 꼬리가 더 두꺼워 p 값이 더 크게 나온다 → 작은 표본에서도 보수적(안전) 판단.

5-1. t 분포의 모양 감각

 

6. 단계별 계산 예시

가상의 몸무게 데이터 n = 5(kg): 68, 70, 71, 69, 72

모평균 가설

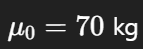
(양측, α = 0.05)

* 여기에서 α 는 유의수준 (귀무가설이 실제로 참일 때, 귀무가설을 기각활 확률)이며, 양측으로 5%이므로 꼬리 한쪽당 0.025 .

 

 

• 평균

  

• 편차·제곱합

• 표본분산·표준편차

• 표준오차

• t-값

• 판정
  • df=4 일 때 양측 α=0.05 임계값 |t| ≈ 2.776
    
    • 이 값은 t-분포 표에서 df=4인 상황에서 한쪽 꼬리 α 0.025에 해당하는 값.

    • 

  • 관측 t=0 < 2.776 → 귀무가설 기각 못 함 (당연히 평균이 같다고 보인다).

참고.

왜 α가 낮으면 신뢰도가 올라간다고 말할까?

위 예시에서 α가 높을수록 |t|값이 올라가서 더욱 참이라고 말할 확률이 올라간다.
그렇다면 오히려 분별을 똑바로 못 하는 것이 아닌가? 라는 의문이 들 수 있다.

여기에서 용어 "신뢰도"를 다시한번 짚고 넘어갈 필요가 있다.
여기에서 신뢰도란 "참인 가설을 참이라고 말할 확률"이다.

거짓을 거짓이라고 말할 확률은 "검정력"이라고 한다.
β로 쓰고, 계산식은 따로 있다...

7. 왜 ‘자유도(df)’가 필요한가?

• 분모의 s 자체가 데이터 5개로부터 추정됐다.
• 평균을 계산하는 과정에서 1개의 제약(“합은 5·X”)이 생겨 독립 정보량이 4개가 됐기에 df = n-1 = 4.
• df가 작을수록 “추정 불확실성”이 커져 t 분포 꼬리가 두꺼워진다.

 

 

이렇게 t - 분포를 통해서 t-value를 구하는 방법을 알아보았다.